Новые возможности расчётной программы T‑FLEX Анализ 18

Автор: Анна Миронова, инженер по тестированию ПО, АО «Топ Системы»

В T‑FLEX Анализ 18 реализована расширенная поддержка современных материалов – пластических, гиперупругих и композитных, – которая допускает физическую нелинейность, учитывает большие перемещения, направленность свойств и сложную структуру материалов.

В условиях стремительного развития инженерных технологий и усложнения конструкций особую роль в расчётных программах приобретает корректное и реалистичное моделирование материалов. Сегодня от точности описания их физико-механических свойств напрямую зависят надёжность, безопасность и конкурентоспособность создаваемых изделий. Использование современных моделей материалов позволяет перейти от упрощённых расчётных схем к полноценному анализу реального поведения конструкций в рабочих и предельных режимах. В T‑FLEX Анализ 18 стала доступна расширенная поддержка современных материалов – пластических, гиперупругих и композитных, – которая допускает физическую нелинейность, учитывает большие перемещения, направленность свойств и сложную структуру материалов.

Добавление новых моделей материалов значительно повышает достоверность результатов численного моделирования, снижает необходимость дорогостоящих натурных испытаний и позволяет выявлять потенциальные проблемы ещё на этапе цифрового проектирования. В итоге достигается не только технический, но и существенный экономический эффект за счёт оптимизации конструкций и сокращения сроков разработки.

Современные инженерные конструкции всё чаще работают на пределе возможностей материалов: перегрузки, ударные воздействия, контактные деформации, большие перемещения, сложные эксплуатационные режимы. В таких условиях линейно-упругий расчёт становится лишь грубой оценкой, а не инструментом точного проектирования.

Гиперупругие материалы

Гиперупругие материалы – изотропные материалы с низкой жесткостью, возвращающиеся в исходное положение после значительного изменения своих форм и размеров под действием нагрузок. В процессе деформирования такие материалы меняют свои жёсткостные свойства, из-за чего зависимость напряжений от деформаций материалов является нелинейной. Поддержка гиперупругости впервые появилась в T‑FLEX Анализ 17, однако в новой версии программы функциональность значительно доработана и добавлены несколько новых моделей гиперупругих материалов (рисунок 1).

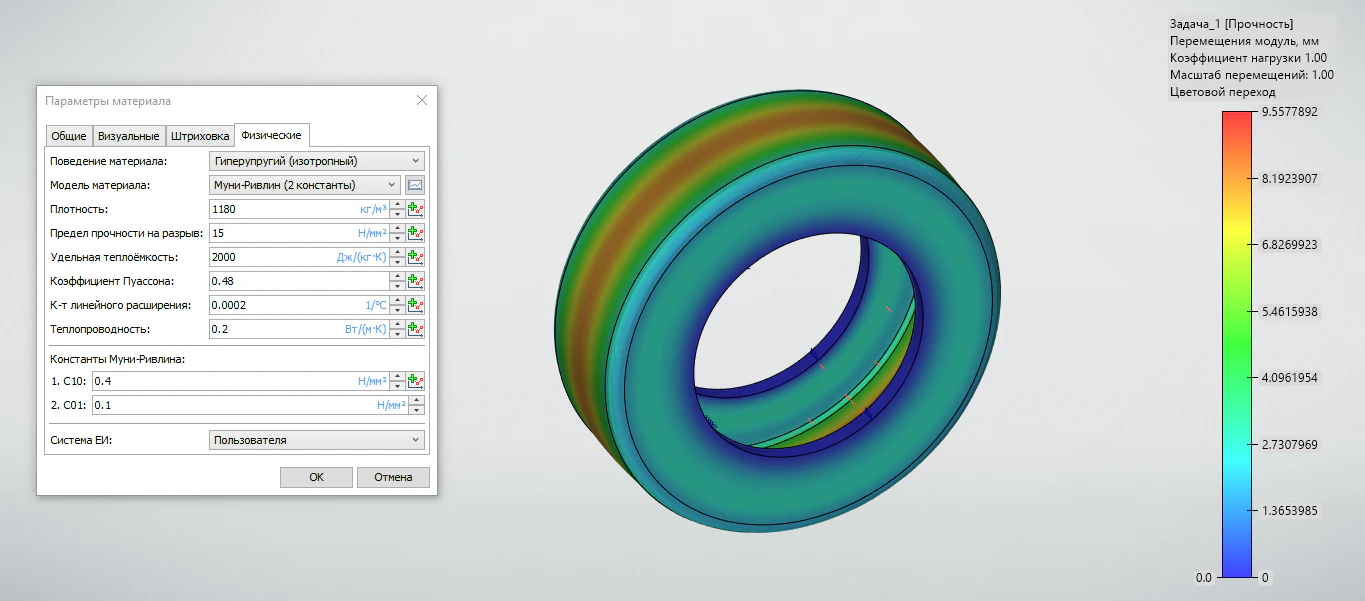
Рисунок 1 – Результаты расчета модели шины в T‑FLEX Анализ 18 с заданием гиперупругой модели материала

Для резин, эластомеров, полимеров и биологических тканей классическая теория упругости неприменима. Здесь необходима гиперупругость, где напряжения выводятся из потенциальной энергии, что позволяет корректно учитывать:

• большие растяжения;
• большие повороты;
• нелинейную связь между напряжением и деформацией.

В T‑FLEX Анализ 18 реализована поддержка гиперупругих моделей материалов (рисунок 2):

• модель Нео-Гука;
• модели Муни-Ривлина (2, 5 и 9 констант);
• модель Блатц-Ко.

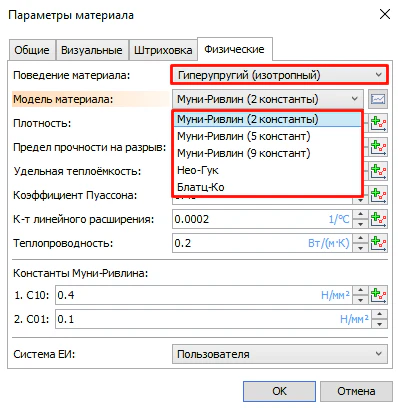
Рисунок 2 – Доступные модели гиперупругих материалов

Модель Нео-Гука — базовая гиперупругость

Простая, устойчивая и быстрая модель. Применяется для большинства стандартных резин и эластомеров, когда деформации модели находятся в диапазоне до 30-40%, а чистый сдвиг до 80-90%. В данной модели используется постоянный модуль сдвига.

Модель материала Нео-Гука применима, когда:

• важна расчётная устойчивость;
• требуется быстрый прогноз деформации;
• деформации большие, но без сложных эффектов упрочнения.

Модель Муни-Ривлина — высокая точность при больших деформациях

В данной модели поддерживаются:

• 2 константы (C10, C01) – для стандартных уплотнений. Хорошо описывает диапазон деформаций 90-100%, но хуже подходит для расчетов модели на сжатие и описания эффектов жёсткости материала;
• 5 констант (C10, C01, C20, C11, C02) – для более сложных нагружений, лучше всего совместима со случаями 90-100% деформации;
• 9 констант (C10, C01, C20, C11, C02, C30, C21, C12, C03) – для максимально точного воспроизведения экспериментальных кривых, однако требует большого количества параметров для описания материала.

Модели гиперупругих материалов Муни-Ривлина позволяют:

• точно рассчитать контакт резиновых уплотнений;
• прогнозировать жёсткость при больших деформациях;
• оптимизировать форму и посадочные размеры.

Модель Блатц-Ко – гиперупругость для сжимаемых резин

Модель Блатц-Ко — модель гиперупругого материала, наиболее подходящая для сжимаемых и пористых материалов. Позволяет учитывать реальное изменение объёма, что невозможно в классических моделях резины. Данная модель проста для использования, поскольку не требует большого количества задаваемых параметров.

Модель материала Блатц-Ко наиболее применима для:

• вспененных эластомеров;
• пористых полимеров;
• газонаполненных демпферов.

Задание экспериментальных данных и других графиков зависимостей

Для всех описанных моделей гиперупругих материалов доступно задание экспериментальных данных в формате «Напряжения - деформации» при заданной температуре (рисунок 3). Свойства таких материалов сильно зависят от температуры. Без учета этой зависимости модель корректно описывает поведение резин только при одной температуре, при которой были подобраны константы.

Ввод экспериментальных данных не обязателен, но их учет позволяет:

• выполнить расчет констант материала;
• учитывать размягчение или упрочнение материала при нагреве и охлаждении;
• корректно рассчитывать контактные напряжения и жёсткость в широком температурном диапазоне;
• получать достоверные результаты анализа при реальных эксплуатационных режимах;
• избегать ошибок при расчётах шин, уплотнений и демпферов, работающих при изменяющейся температуре;
• приблизить модель материала к инженерно достоверной.

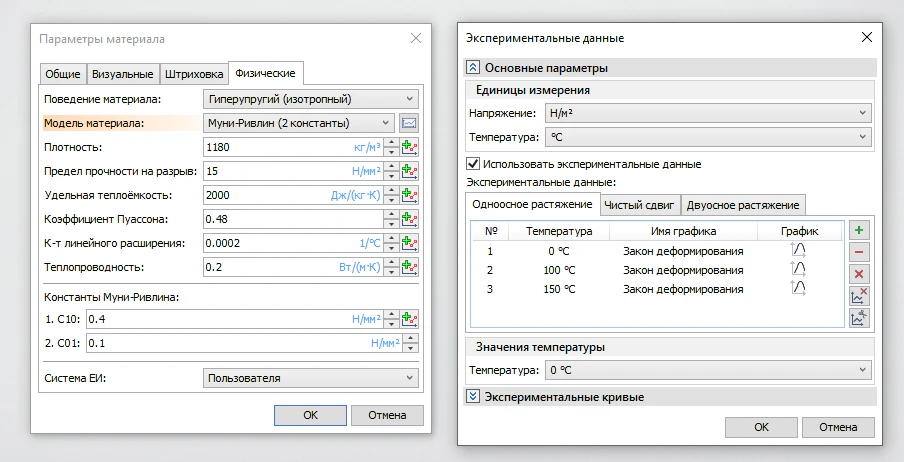
Рисунок 3 – Задание экспериментальных данных

В T‑FLEX Анализ 18 возможно задать различные графики экспериментальных данных для одноосного растяжения, чистого сдвига и двуосного растяжения при конкретной температуре, после чего вывести все расчетные данные на один график для сравнения аппроксимации с точными данными с помощью опции «Экспериментальные кривые» (рисунок 4).

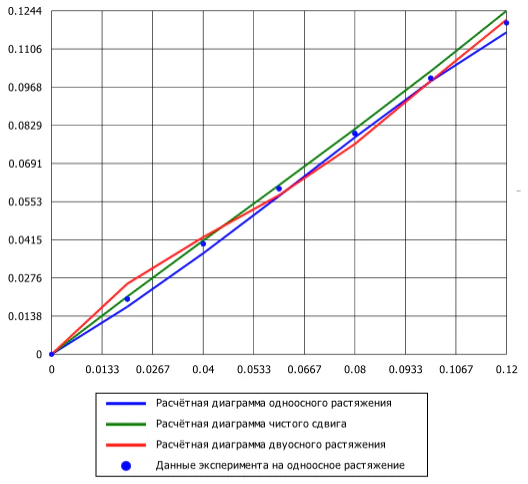
Рисунок 4 – Группа «Экспериментальные кривые»

Помимо этого, для параметров гиперупругих материалов доступен ввод их зависимости от температуры (рисунок 5). Задание таких графиков также повышает точность расчётов и максимально приближает результаты к реальности.

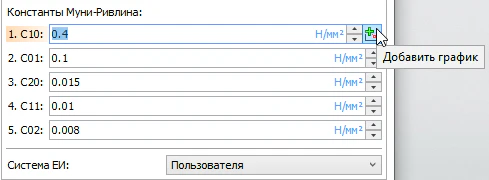
Рисунок 5 – Задание графиков зависимости констант от температуры

При задании зависимостей параметров от температуры необходимо учитывать их изменение при одной и той же температуре.  Это удобно анализировать и отслеживать в общей таблице и на общей расчетной диаграмме (рисунок 6).

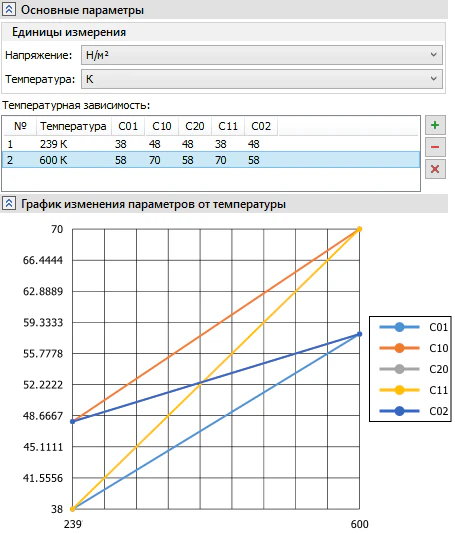
Рисунок 6 – Задание зависимости параметров гиперупругости от температуры

Расширение возможностей расчёта эластичных конструкций

Поддержка гиперупругих моделей выводит расчёты эластомеров и полимеров на качественно новый уровень. Инженер получает возможность учитывать большие обратимые деформации, сложное нелинейное поведение и изменение жёсткости материала в процессе изменения нагрузок. Это позволяет отказаться от грубых упрощений и перейти к реалистичному анализу резиновых, полимерных и биомеханических элементов, в условиях, максимально приближенных к эксплуатационным.

Благодаря этому открываются широкие возможности для оптимизации формы и конструкции изделий, повышения их надёжности и ресурса, а также для виртуальной отработки предельных режимов без проведения трудоёмких и дорогостоящих испытаний. Гиперупругие модели становятся полноценным инструментом инженерного анализа современных изделий из эластичных материалов.

Пластичные материалы

Пластичность – способность материала воспринимать большие деформации при напряжениях, превышающих предел текучести, при этом не разрушаясь. Применение пластичности позволяет выйти за рамки упругой зоны и исследовать поведение конструкции.

В T‑FLEX Анализ 18 стало доступно задание материалам пластичных свойств, что позволяет значительно расширить область применения расчетов и их точность в ряде случаев (рисунок 7).

Пластическое поведение материалов позволяет:

• получать физически корректные результаты при перегрузках и больших деформациях;
• повысить достоверность расчётов;
• проводить проектирование по реальному предельному состоянию.

В T‑FLEX Анализ 18 реализованы две модели пластичных материалов: билинейная и мультилинейная, благодаря чему возможно реализовывать решение широкого спектра инженерных задач.

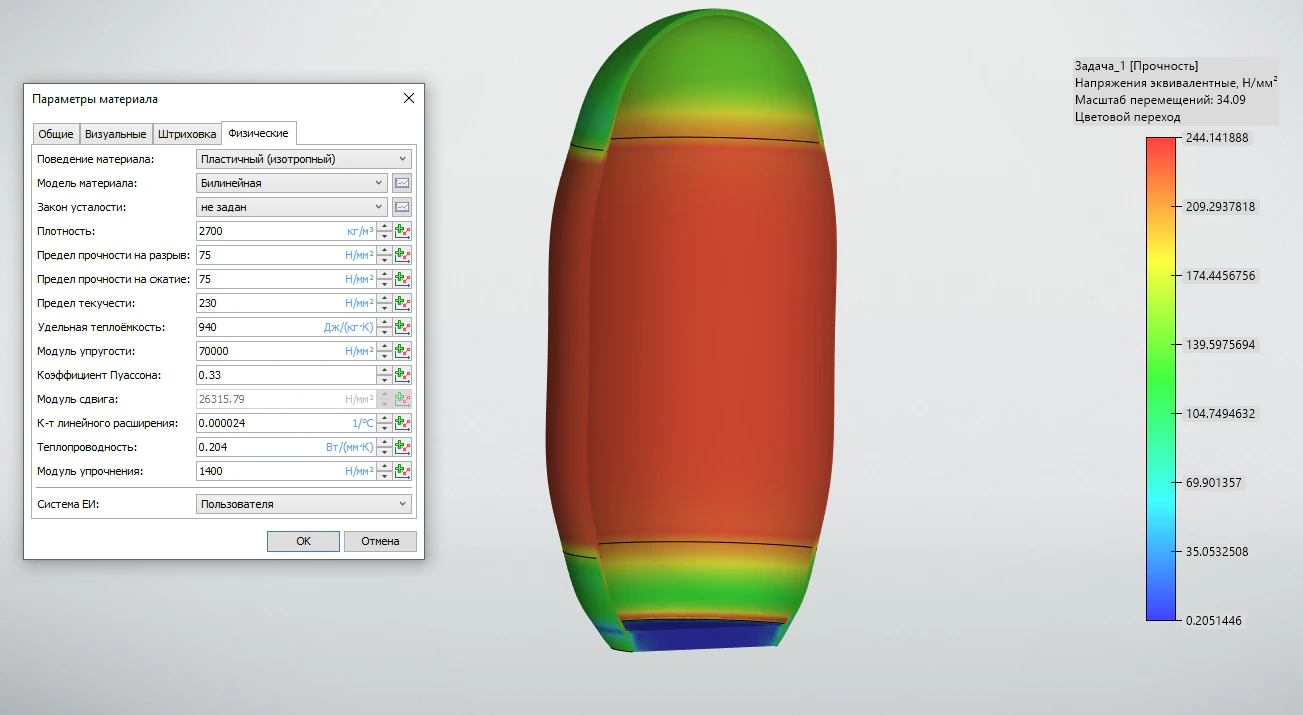
Рисунок 7 – Результаты расчета баллона с пластичными свойствами, нагруженного изнутри

Билинейная модель — быстрый и наглядный анализ пластичности

Билинейная модель пластичности — это упрощённая, но практичная концепция, широко используемая в инженерном анализе для моделирования поведения металлов. Она идеально подходит для задач, где важна общая прочность и энергопоглощение конструкции, а не детали сложного упрочнения материала. Модель представляет поведение материала двумя прямыми линиями: первая описывает идеально упругую область, где деформации полностью обратимы, а вторая — область пластического течения, где после снятия нагрузки остаётся постоянная деформация (рисунок 8).

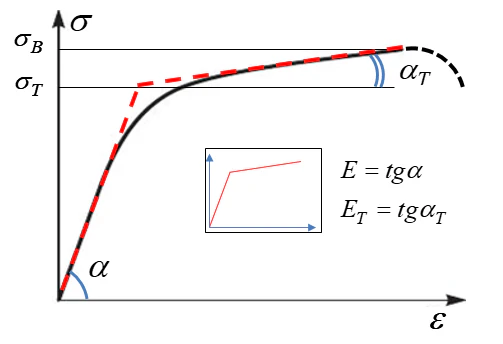
Рисунок 8 – Диаграммы деформирования билинейной модели пластичности.

Кривая чёрного цвета – реальная диаграмма деформирования. Кривая красного цвета – аппроксимированная билинейной моделью диаграмма деформирования.

Основная идея в том, что после достижения предела текучести материал деформируется уже с новой, обычно меньшей, «кажущейся» жёсткостью, что позволяет пользователю эффективно оценить пластические деформации и остаточные напряжения в элементах конструкций при перегрузках, ударных воздействиях или в зонах концентрации напряжений.

Для задания пластичного материала необходимо ввести особый параметр – модуль упрочнения. Есть возможность задания зависимости от температуры в случае, если на модель также прикладывается тепловая нагрузка, что является распространенным случаем при расчетах металлических конструкций (рисунок 9).

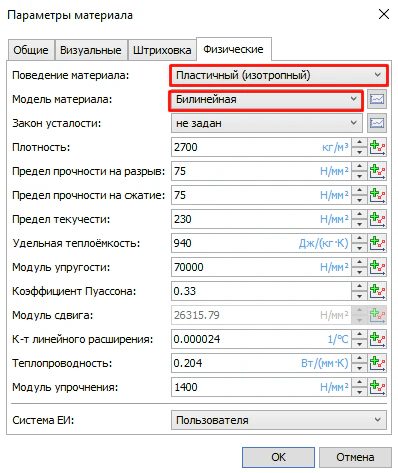
Рисунок 9 – Параметры, требуемые для задания билинейной модели пластичности

После ввода модуля упрочнения и предела текучести становится доступным просмотр диаграммы деформированного состояния, на которой наглядно показаны два участка различного поведения материала.  Первый участок соответствует упругой зоне и характеризуется модулем упругости, второй – пластической зоне и характеризуется модулем упрочнения (рисунок 10).

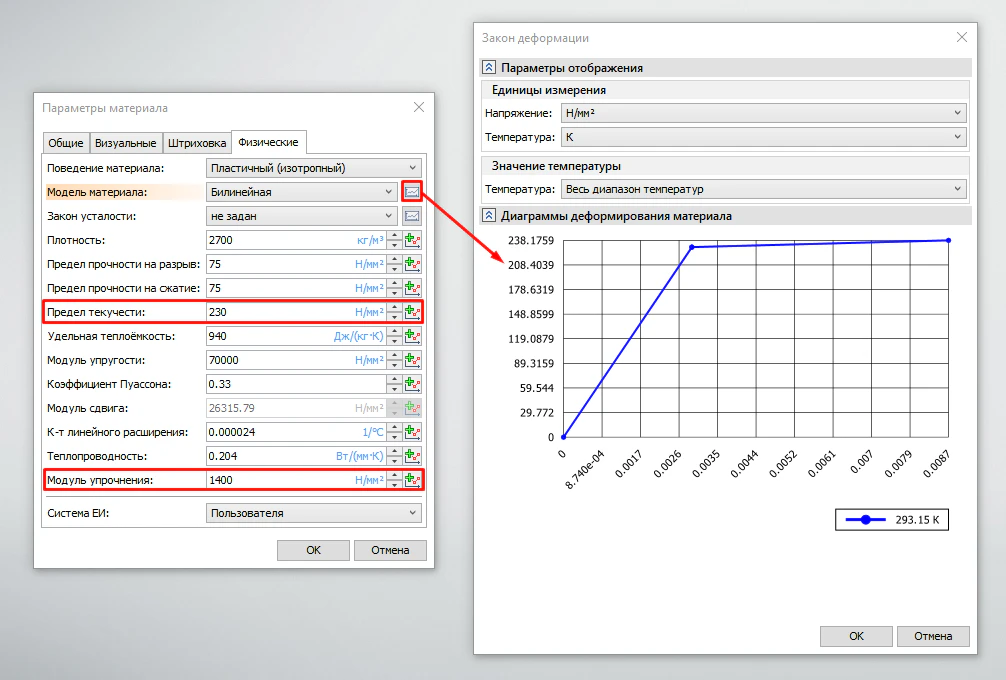
Рисунок 10 – Вывод диаграммы деформированного состояния материала

Возможности расчета с билинейной моделью материала на практике:

• определение момента начала пластических деформаций;
• отслеживание роста пластической зоны;
• расчёт остаточной деформации после разгрузки;
• оценка реального запаса по несущей способности, а не условный коэффициент.

Всё это важно для металлоконструкций, работающих в режиме временных перегрузок и аварийных воздействий.

Мультилинейная модель — максимальная близость к эксперименту

Мультилинейная модель пластичности — это развитие билинейной модели, которое позволяет гораздо точнее описывать реальное поведение материалов, особенно их фазу упрочнения. Если билинейная модель аппроксимирует пластическую область одной прямой, то мультилинейная использует серию прямолинейных отрезков, следуя за экспериментальной кривой «напряжение - деформация» (рисунок 11).

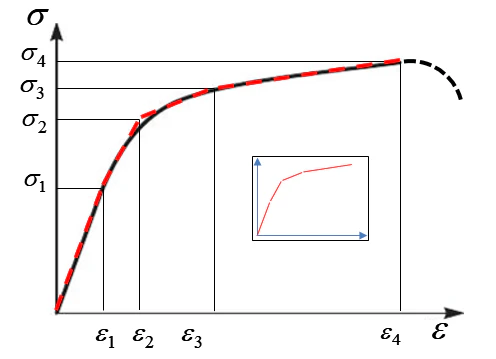
Рисунок 11 – Диаграммы деформирования мультилинейной модели пластичности. Кривая чёрного цвета – реальная диаграмма деформирования. Кривая красного цвета – аппроксимированная мультилинейной моделью диаграмма деформирования

Точность данной модели делает её незаменимой для задач, где критически важно корректно смоделировать постепенное изменение жёсткости материала после текучести: при анализе пластических деформаций в зонах локальных перегрузок, прогнозировании усталостной долговечности или расчёте энергопоглощения при прогрессирующем смятии. По сути, она предлагает разумный компромисс между простотой линейных моделей и полнотой сложных нелинейных кривых, значительно повышая точность инженерного анализа без чрезмерного усложнения вычислений.

Пользователь может задать любое количество узлов диаграммы — от простых до полностью повторяющих экспериментальные испытания.

По аналогии с другими параметрами материалов, имеется возможность задать несколько диаграмм деформирования материала для описания поведения материала при различных температурах, что может быть крайне важно при анализе прочности и несущей способности конструкции (рисунок 12).

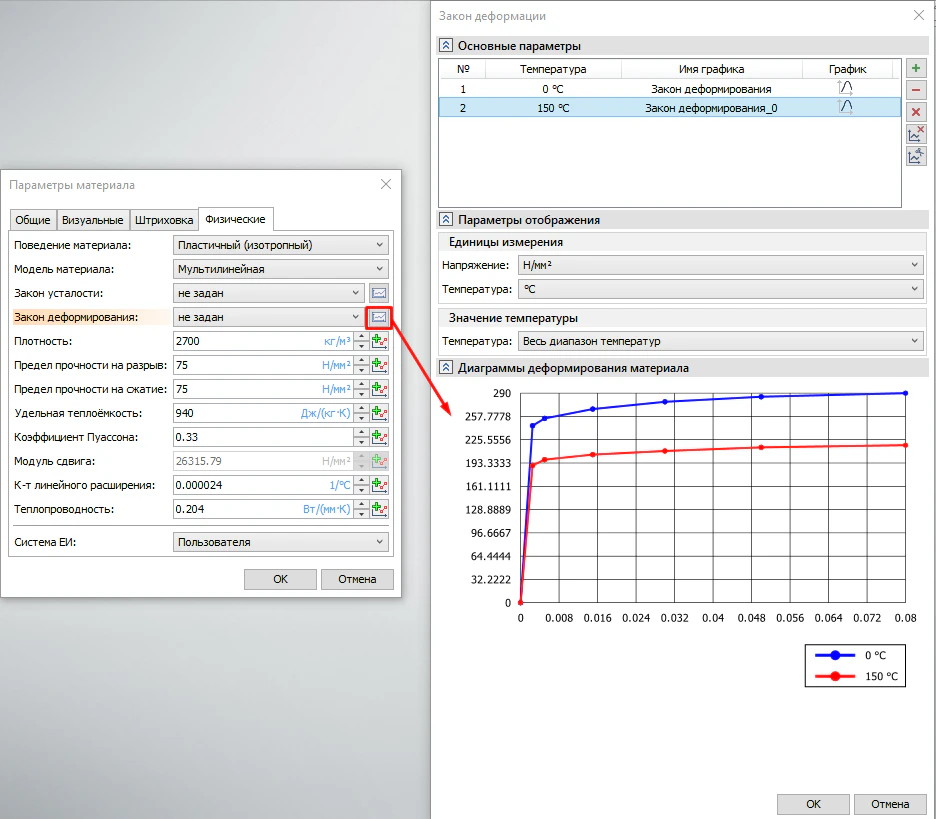
Рисунок 12 – Задание диаграмм деформированного состояния материала для различных температур

Преимущества использования мультлинейной модели пластичности:

• точное воспроизведение площадки текучести;
• корректный учёт стадии упрочнения;
• высокая достоверность при сложных циклах нагружения;
• возможность анализа локального перераспределения напряжений.

Дополнительная функциональность процессинга и постпроцессинга

При использовании пластичного материала в списке результатов появятся дополнительные варианты для выбора – интенсивность пластических деформаций и полные деформации, являющиеся уникальными для расчетов с использованием пластичности (рисунок 13).

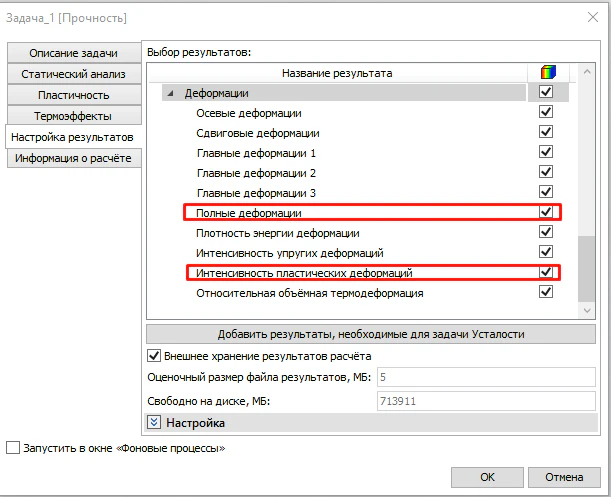
Рисунок 13 – Дополнительные результаты – интенсивность пластических деформаций и полные деформации

Интенсивность упругих деформаций позволяет оценить степень и масштаб необратимых деформаций модели, а полные деформации — суммарную величину и распределение всей накопленной деформации в конструкции — как упругой (обратимой), так и пластической (необратимой).

Визуализация и численные данные, полученные после расчета, дают возможность проанализировать повреждения материала и остаточную несущую способность (рисунок 14).

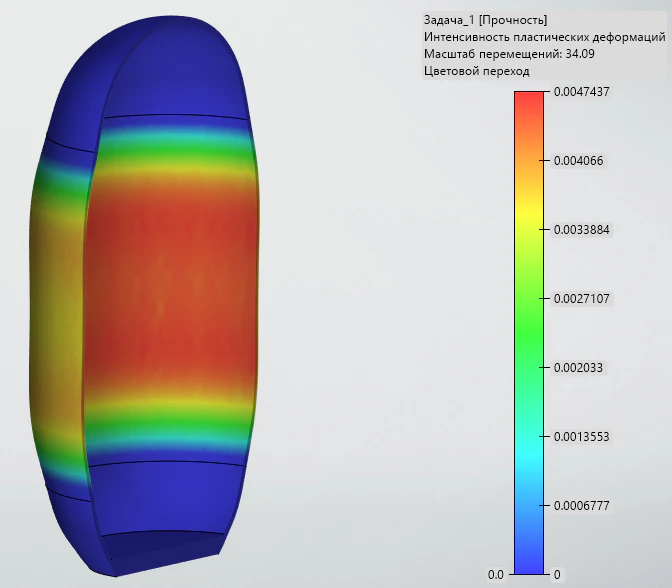
Рисунок 14 – Интенсивность пластических деформаций на баллоне, нагруженном давлением изнутри

Инженерный анализ за пределом упругости

Переход от классических упругих моделей к билинейному и, в особенности, мультилинейному описанию пластичности стал важным этапом развития инженерного анализа. Эти модели материалов позволяют проанализировать поведение конструкции после наступления текучести. Пользователь получает инструмент для оценки несущей способности по предельному состоянию, а не только по условиям упругости. Главное преимущество — это возможность точно предсказывать реальное поведение металлических узлов, моделируя процессы перераспределения усилий и поглощения энергии за счет контролируемых пластических деформаций.

С появлением удобных инструментов для задания многоточечных кривых деформирования открылись новые возможности для повышения точности и достоверности расчетов. Мультилинейная модель, учитывающая фазу упрочнения, позволяет смоделировать сложные процессы: от анализа остаточных напряжений после деформирования.

Композиционные материалы

Современные инженерные изделия всё чаще создаются не из однородных материалов, а из композитов, где свойства формируются не только материалом, но и структурой слоёв, ориентацией волокон и составом компонентов.

В T‑FLEX Анализ 18 реализована возможность расчёта слоистых композиционных материалов с графическим отображением получившихся свойств пакета Это значительно расширяет возможности проведения различных типов расчетов для пользователя (рисунок 15).

В качестве геометрии при задании композиционных материалов можно использовать грани или поверхности.

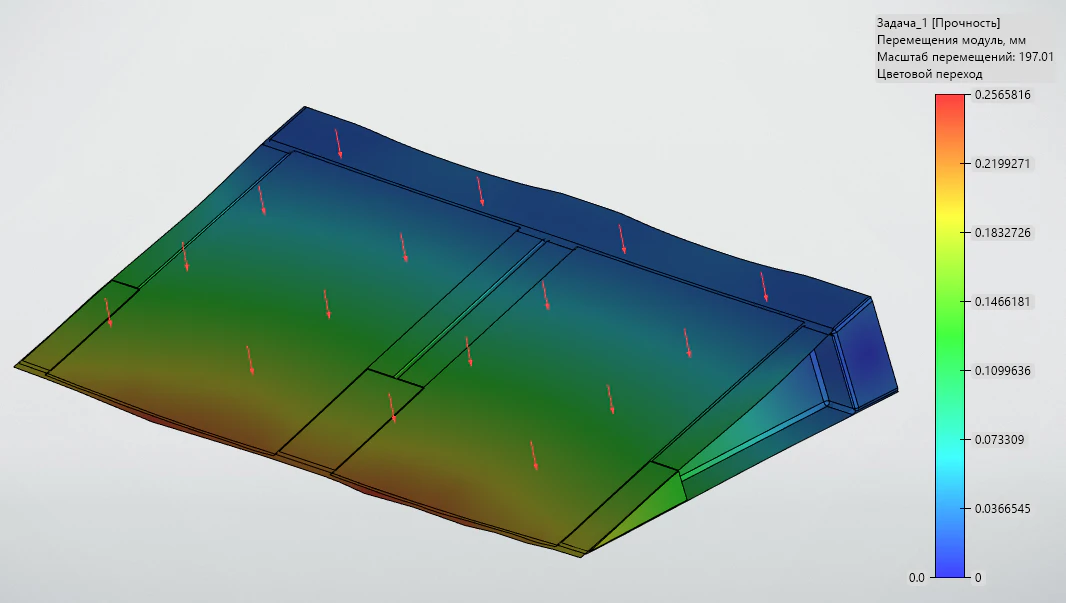
Рисунок 15 – Отображение результата на модели интерцептора с композитной верхней панелью

Поддержка слоистых композиционных материалов позволяет проектировать и анализировать конструкции из:

• углепластиков;
• стеклопластиков;
• органопластиков;
• и других многослойных материалов.

Два уровня работы с композитами: монослой и многослойная структура

В T‑FLEX Анализ 18 реализована двухуровневая концепция описания композитных материалов (рисунок 16):

1. Монослой — строительный элемент композита, который также может использоваться в качестве самостоятельного материала.
2. Многослойный материал — сформированный пакет с автоматическим расчётом итоговых свойств.

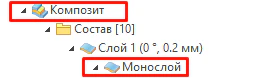
Рисунок 16 – Отображение части состава многослойного композита, состоящего из монослоёв

Такой подход полностью соответствует реальной технологии производства композитных конструкций и позволяет реализовать расчет большого спектра различных материалов.

Монослой

Монослой представляет собой отдельный слой материала, который может быть как самостоятельным однонаправленным композитом, так и составляющим многослойного материала.

Каждый монослой может быть задан как:

• изотропный — одинаковые свойства во всех направлениях;
• ортотропный — различные модули упругости, коэффициенты Пуассона и прочностные характеристики по главным осям;
• трансверсально-изотропный - материал, у которого свойства одинаковы во всех направлениях в одной плоскости (например, в плоскости слоя), но отличаются в направлении, перпендикулярном этой плоскости (по нормали).

Это позволяет моделировать как простые полимерные слои, так и армированные однонаправленные структуры.

Физические свойства монослоя являются обязательными для ввода пользователем – исходя из них при составлении многослойного композита будут рассчитываться конечные свойства композита (рисунок 17).

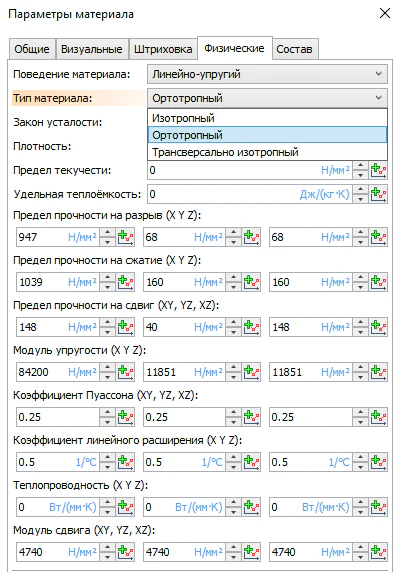
Рисунок 17 – Физические свойства монослоя

Ещё одним обязательным для ввода параметром является состав монослоя. В состав монослоя может входить любое количество наполнителей и матрицы, которые могут быть заданы как изотропными, так и другими типами материалов. Для анизотропных составляющих в рамках задания материала можно задать угол укладки, который также будет учтен при «выкладке» монослоя в итоговом композите, позволяя управлять жёсткостью конструкции, направленностью прочности и перераспределением напряжений (рисунок 18).

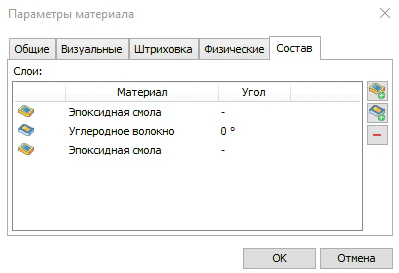
Рисунок 18 – Состав монослоя, включающий в себя матрицу и наполнитель

Реализованные возможности работы с композитами особенно важны при:

• разработке новых материалов;
• оптимизации состава;
• анализе чувствительности характеристик к изменению компонентов.

Многослойный материал

Многослойный материал формируется из набора различных слоёв, которыми могут являться как монослои или другие многослойные композиты, так и любые другие материалы (ранее созданные или добавленные из «Библиотеки материалов») (рисунок 19, 20).

При этом программа автоматически вычисляет все эффективные физические свойства композита на основе:

• свойств каждого слоя;
• толщины слоёв;
• углов ориентации;
• порядка укладки.

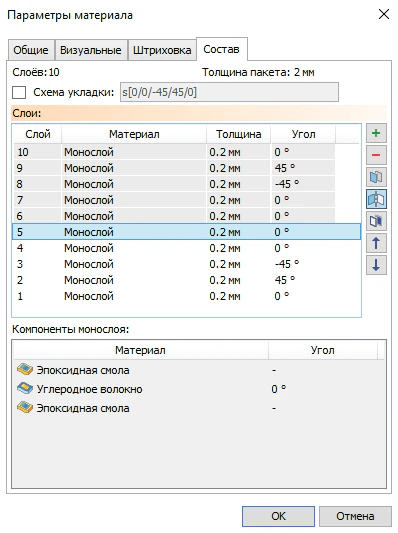
Рисунок 19 – Состав многослойного композита

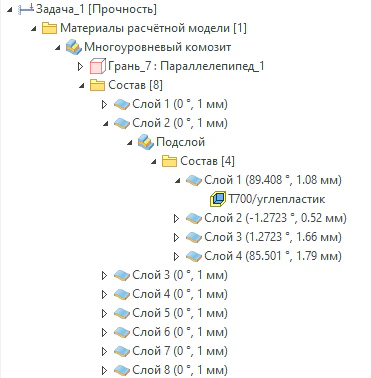
Рисунок 20 – Состав многоуровневого композита

При работе с составом материала пользователь может задать угол укладки каждого слоя, толщину, при необходимости задать симметричную укладку, дублировать или инвертировать какие-либо слои.

Для удобства отслеживания свойств монослоя при задании композита есть возможность просмотреть компоненты каждого слоя.

При расчёте многослойного материала программа учитывает:

• анизотропию каждого слоя;
• влияние угла укладки на прочность;
• различие растяжения, сжатия и сдвига;
• вклад каждого слоя в общую жёсткость конструкции.

Это позволяет анализировать реальное поведение композитных конструкций, а не приближённые эквивалентные модели.

После задания композитного материала можно визуально оценить корректность схемы укладки слоев с возможностью вывода необходимых параметров слоя (рисунок 21).

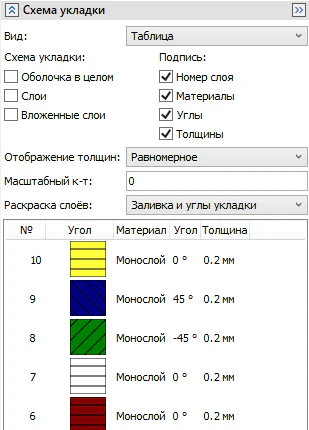
Рисунок 21 – Схема укладки композита

Для проверки физических параметров готового пакета есть возможность отобразить полярную диаграмму упругих свойств получившегося многослойного композита (рисунок 22).

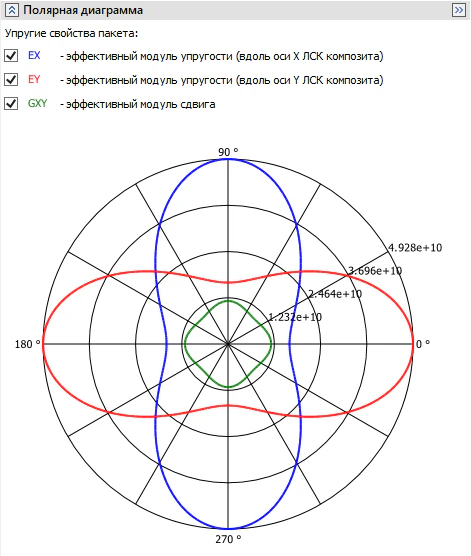
Рисунок 22 – Визуализация полярной диаграммы

При задании композитного материала для какого-либо элемента расчетной модели автоматически присваивается гипотеза – теория многослойных пластин, которая определяет методы расчета модели. Проверить присвоение нужной гипотезы можно в диалоге создания задачи (рисунок 23).

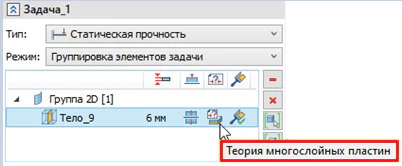
Рисунок 23 – Теория многослойных пластин

В окне «Расчет» добавляются уникальные результаты, доступные только для композитных элементов расчетной модели – специальные коэффициенты запаса (рисунок 24).

Рисунок 24 – Коэффициенты запаса для композиционных материалов

Коэффициент запаса по максимальным напряжениям – простой критерий, показывающий, какое из напряжений или деформаций первым превысит допуск.

Коэффициент запаса по критерию Цая-Хилла – учитывает взаимодействие напряжений в ортотропном слое. Эффективен для материалов с равной прочностью на растяжение и сжатие.

Коэффициент запаса по критерию Цая-Ву – наиболее универсальный тензорный полиномиальный критерий. Учитывает различие прочностей на растяжение и сжатие и их взаимодействие.

Коэффициент запаса «Минимальный» – при расчете находится глобальный минимум коэффициента запаса по всей конструкции и всем слоям, указывая на самое слабое место. Значение меньше единицы указывает на предполагаемое разрушение.

Работа постпроцессора при анализе композитов имеет критическую важность, поскольку только на этом этапе сложные результаты расчётов переводятся в удобную и наглядную форму, необходимую для принятия решений о прочности и оптимизации конструкции.

При отображении ряда результатов доступны особые типы отображения композитных оболочек:

• Огибающая эпюра – для многослойных оболочек в каждой точке эпюры отображается минимальное (в случае коэффициента запаса) или максимальное (для остальных результатов) значение, выбранное среди всех слоев материала. Позволяет определить наихудший случай нагружения (рисунок 25).

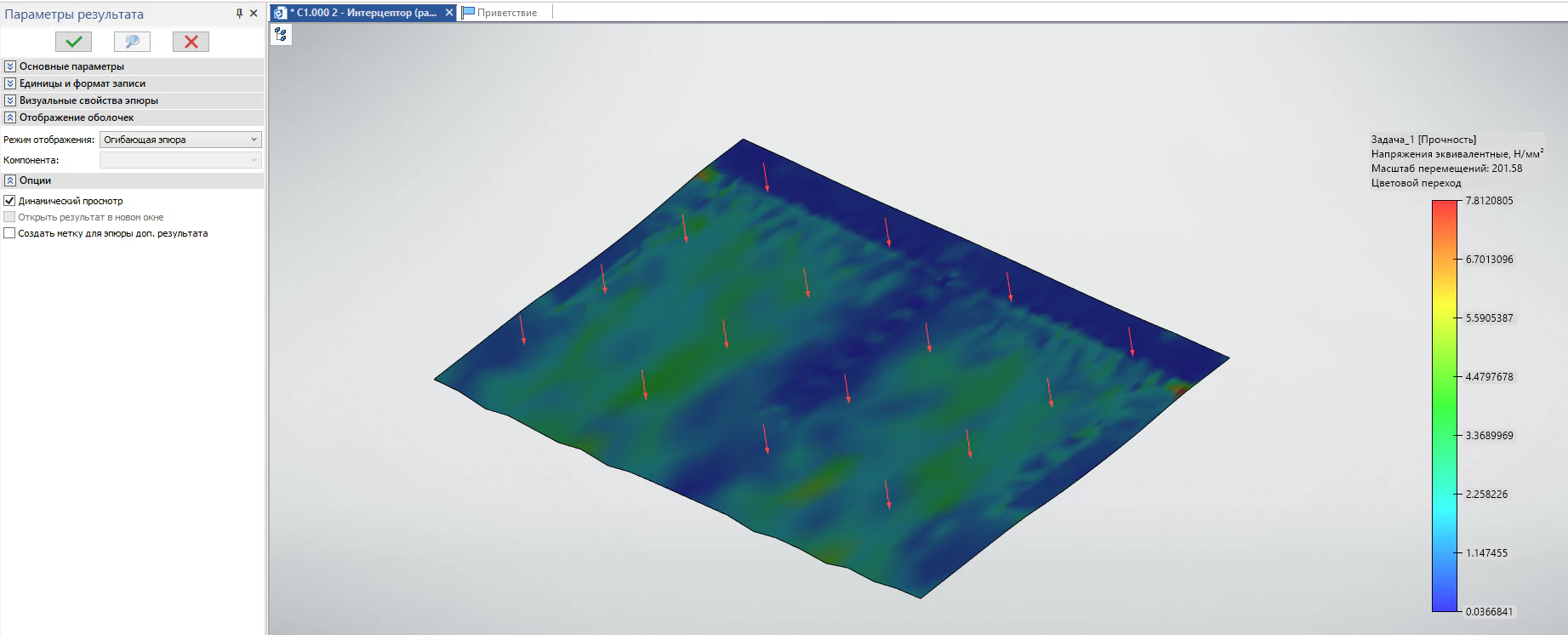
Рисунок 25 – Отображение огибающей эпюры на композитной оболочке

• Оболочка в целом – тип эпюры, на которой многослойные оболочки считаются «эквивалентными» обычным оболочкам. В таком режиме компонента «Верх» - это верх первого слоя композита, а компонента «Низ» – низ последнего слоя композита. Даёт сводную, «усреднённую» картину по всей толщине пакета (рисунок 26).

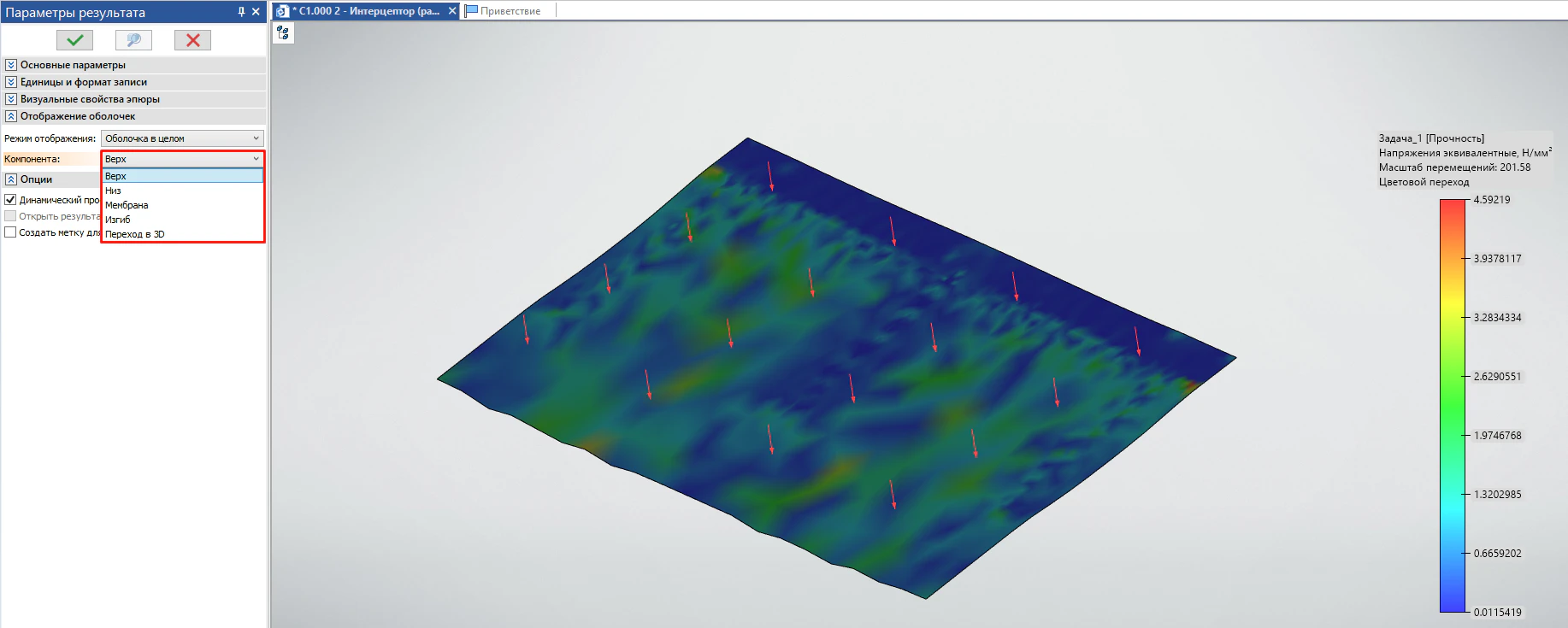
Рисунок 26 – Отображение оболочки в целом на композитной оболочке

• Послойное отображение результатов – эпюра, при использовании которой можно выбрать слои для отображения и их компоненту. Позволяет детально оценить и визуализировать распределение тех или иных параметров по каждому слою (рисунок 27).

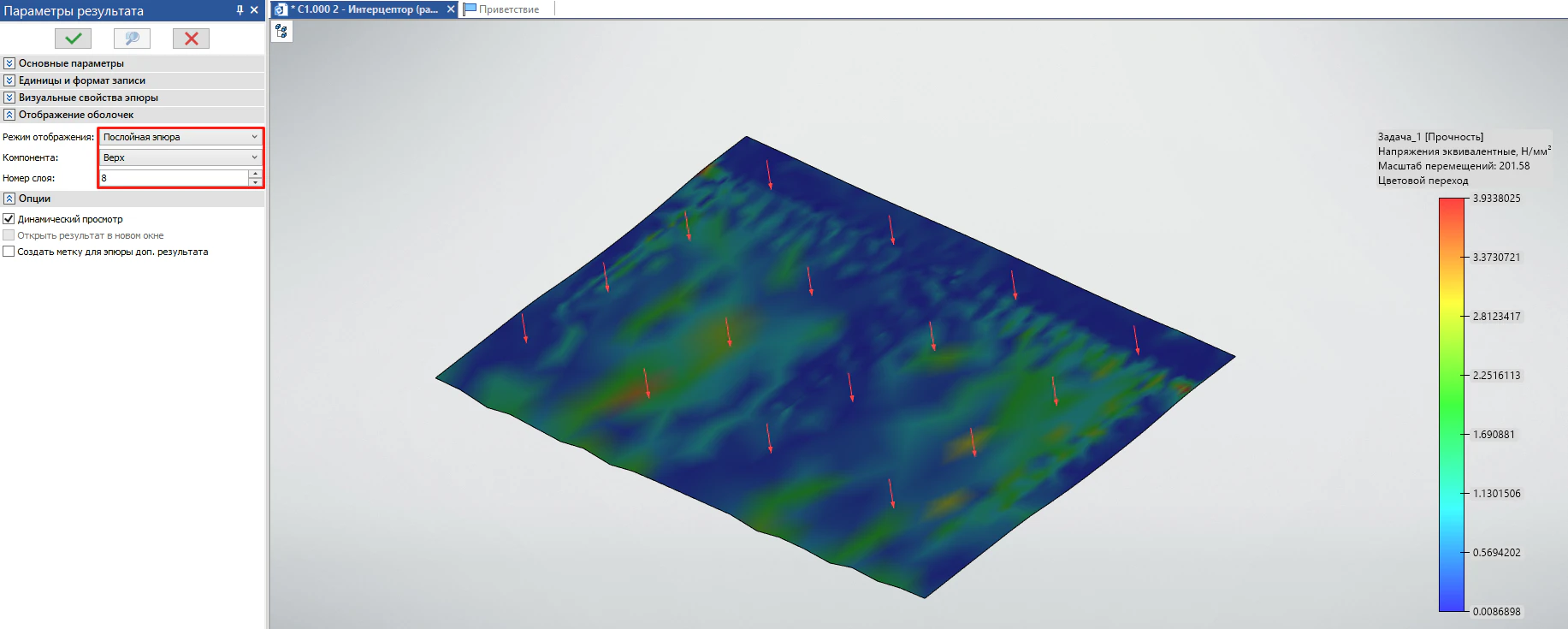
Рисунок 27 – Отображение компоненты выбранного слоя на композитной оболочке

Для уточнения численного результата в конкретной точке на конкретном слое в новой версии программы T‑FLEX Анализ 18 был дополнен инструмент «Локальный результат». С помощью проставления локальных меток можно вывести конкретное значение в интересующем узле модели, что дает возможность более точно анализировать области с высоким шансом разрушения (рисунок 28).

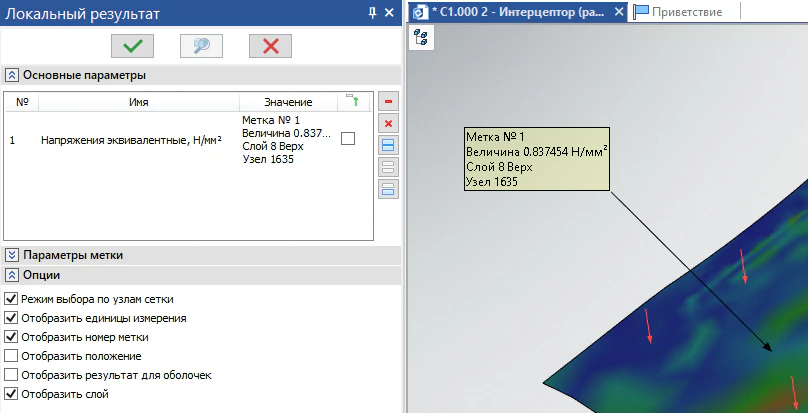
Рисунок 28 – Вывод локального результата для эквивалентных напряжений

Инженерный анализ композитных конструкций

При помощи описанных инструментов пользователь имеет возможность полноценно работать с композиционными материалами и применять их в расчетных моделях. Удобный анализ результатов позволяет точно и наглядно определять несущую способность композитной конструкции, оценить потенциальные разрушения и вывести все необходимые параметры.

Использование композитных материалов в программе даёт принципиально новые возможности:

• проектирование по реальной структуре композита, а не по усреднённым свойствам;
• точный контроль направленной жёсткости и прочности;
• анализ разрушения по отдельным слоям;
• быстрая проверка различных вариантов укладки;
• снижение количества натурных испытаний.

Заключение

Реализация новых моделей материалов – это большой шаг вперёд в развитии программных средств T‑FLEX Анализ 18. Новая версия расширяет спектр проводимых расчётов. Система позволяет не только предсказывать нелинейное поведение конструкций вплоть до разрушения, но и раскрывает потенциал для решения новых инженерных задач моделирования гиперупругого поведения материалов и проектирования лёгких и прочных композитных структур.