Геометрическое ядро RGK – год спустя
Автор: Леонид Баранов, директор по развитию технологий 3D моделирования, АО «Топ Системы»

Прошёл ровно год с момента презентации компанией «Топ Системы» нового продукта – геометрического ядра RGK 2.0. По результатам представления ранее была опубликована статья Геометрическое ядро RGK на форуме компании «Топ Системы». В этой статье мы постараемся рассказать об основных доработках, выполненных в RGK за прошедшее время.
Геометрическое ядро представляет собой программный компонент, предназначенный для решения разнообразных задач геометрического моделирования: построение различными способами твердотельных, поверхностных и каркасных моделей с использованием «точной» геометрии, проведение разного рода анализа на полученных моделях, как то проверка корректности построения, вычисления масс-инерционных характеристик, расстояний, углов, пересечений наборов тел между собой, построения полигональных аппроксимаций точной геометрии, построения проекций с удалёнными невидимыми линиями и т.д. Полный список задач, решаемых ядром RGK, как и его архитектура и особенности представления модели, за прошедший год не претерпели значительных изменений, чего нельзя сказать о функциональности, структуре API и различных прикладных особенностях продукта. Цель данной статьи в том, чтобы рассказать как раз о произошедших изменениях ядра за минувший год. По традиции изменения будут представлены в наиболее наглядном виде – форме иллюстраций, благо геометрическое моделирование очень наглядная и очевидная даже для неспециалистов область прикладной математики.
Функциональность по формированию и редактированию модели
Значительному развитию подверглась функциональность «прямого» моделирования. В частности, в операции «замена граней тела» была добавлена поддержка перестроения сглаживаний, контактирующих с заменяемой гранью. Поддерживаются сглаживания как постоянного, так и переменного радиуса.
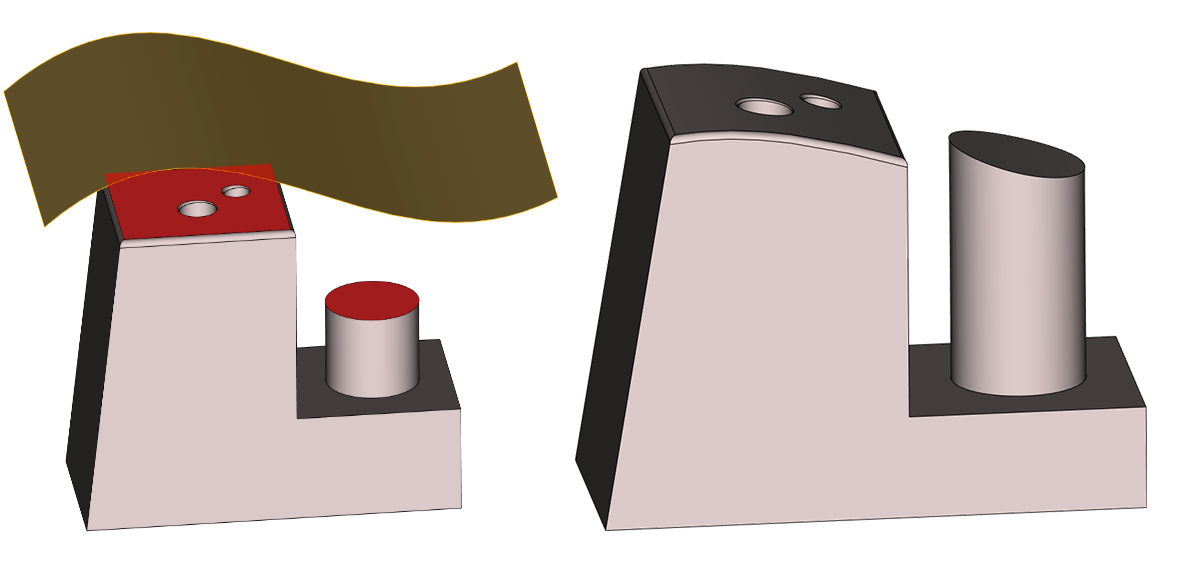
Пример замены поверхностей двух граней на поверхности листового тела (на внутренних отверстиях сглаживание переменного радиуса)
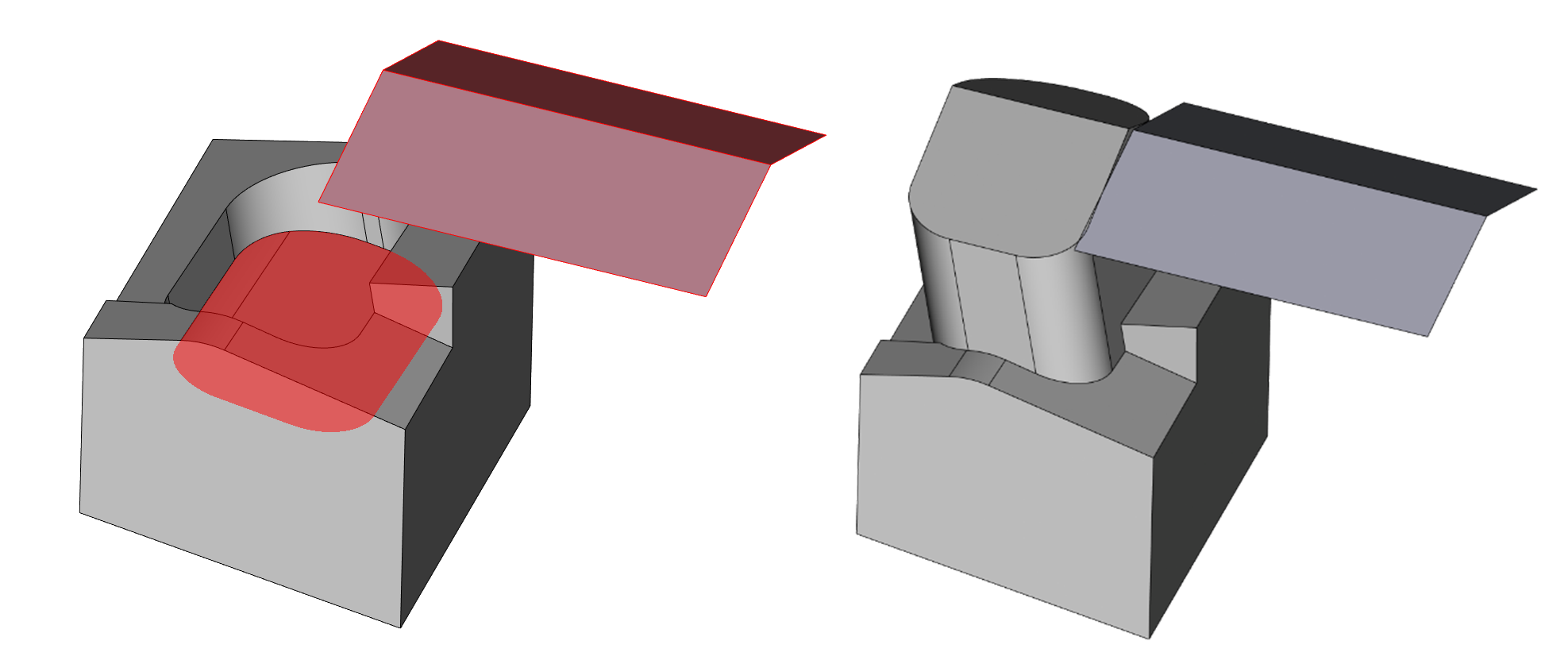
Пример замены грани на листовое тело с несколькими гранями
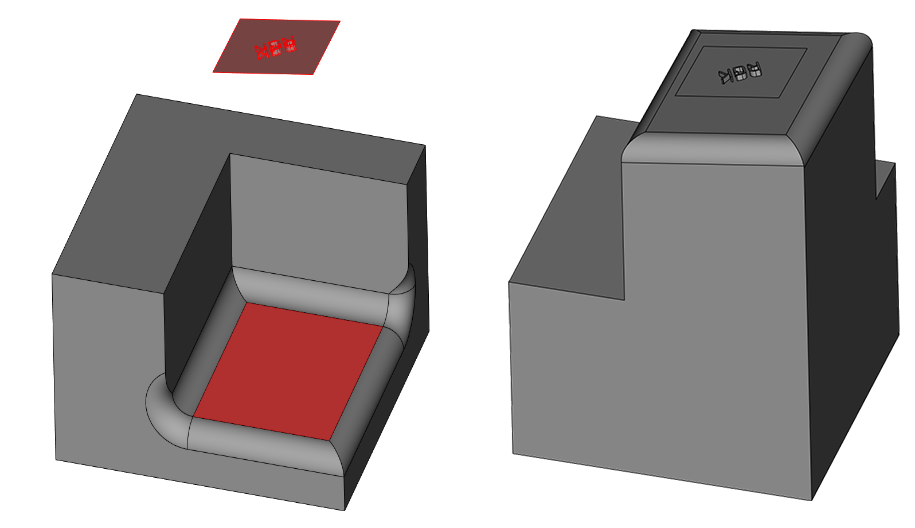
Пример замены граней, контактирующих со сложным сглаживанием
Сами алгоритмы операции были доработаны с целью обеспечения возможности замены несвязанных граней на поверхности из граней произвольного листового тела.
Как частный случай работы этой операции, конечно, поддерживается функциональность изменения размера и положения цилиндрической, сферической, конической и тороидальных граней.

Пример изменения радиуса цилиндрической поверхности отверстия
Значительно расширена функциональность операции удаления граней. Добавлена поддержка сложных топологических связей удаляемых граней.
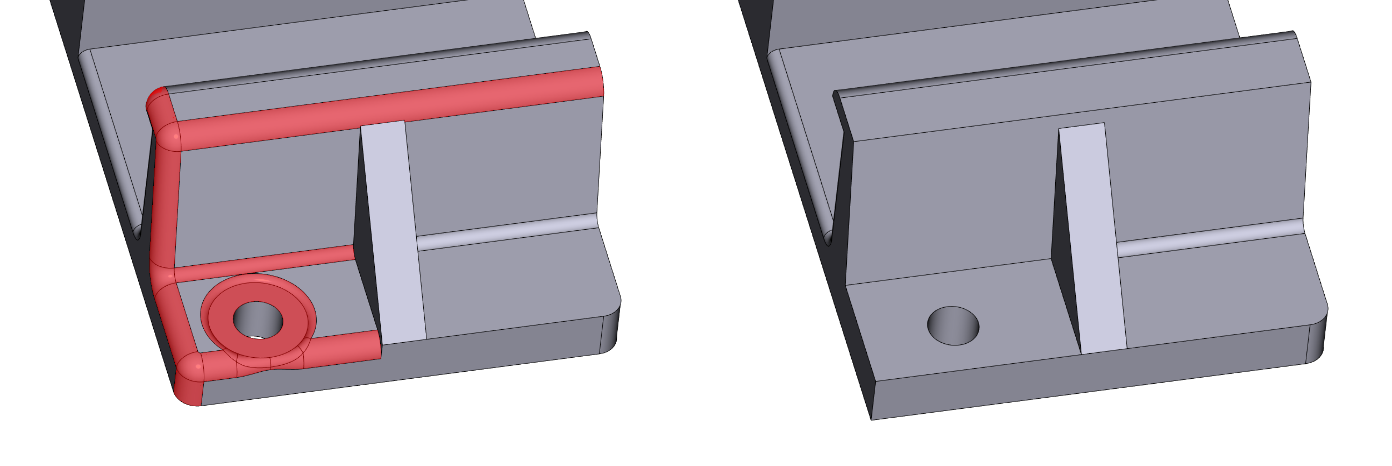
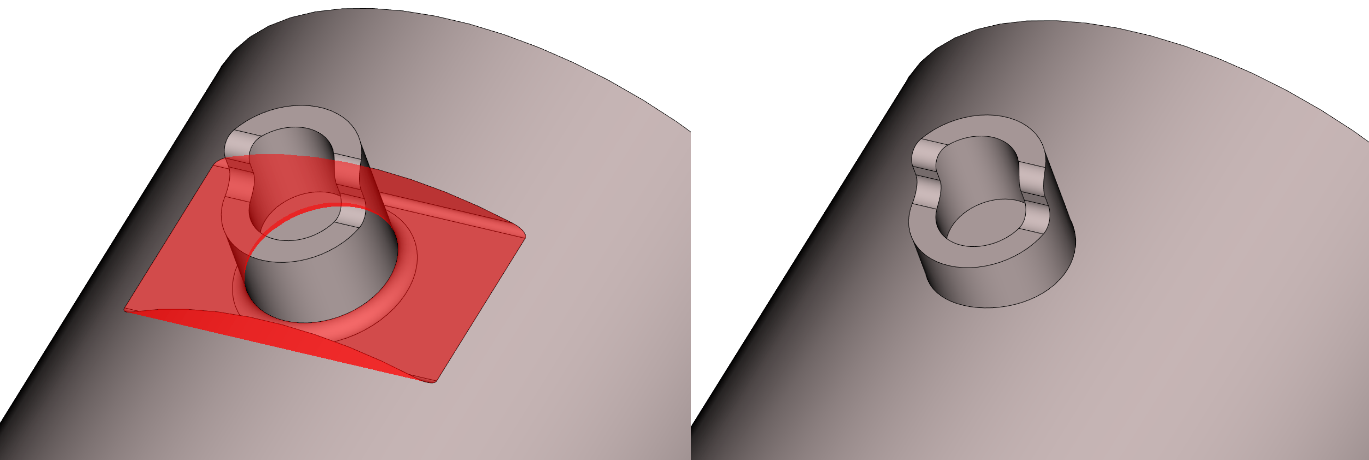
Примеры удаления граней
Разработана новая функциональность распознавания сглаживаний постоянного и переменного радиуса как для отдельных граней, так и для последовательностей. Такая функциональность может быть особенно востребована в приложениях, работающих с импортированной геометрией, так как распознаются поверхности сглаживания как построенные средствами самого RGK, так и импортированные из внешних систем.
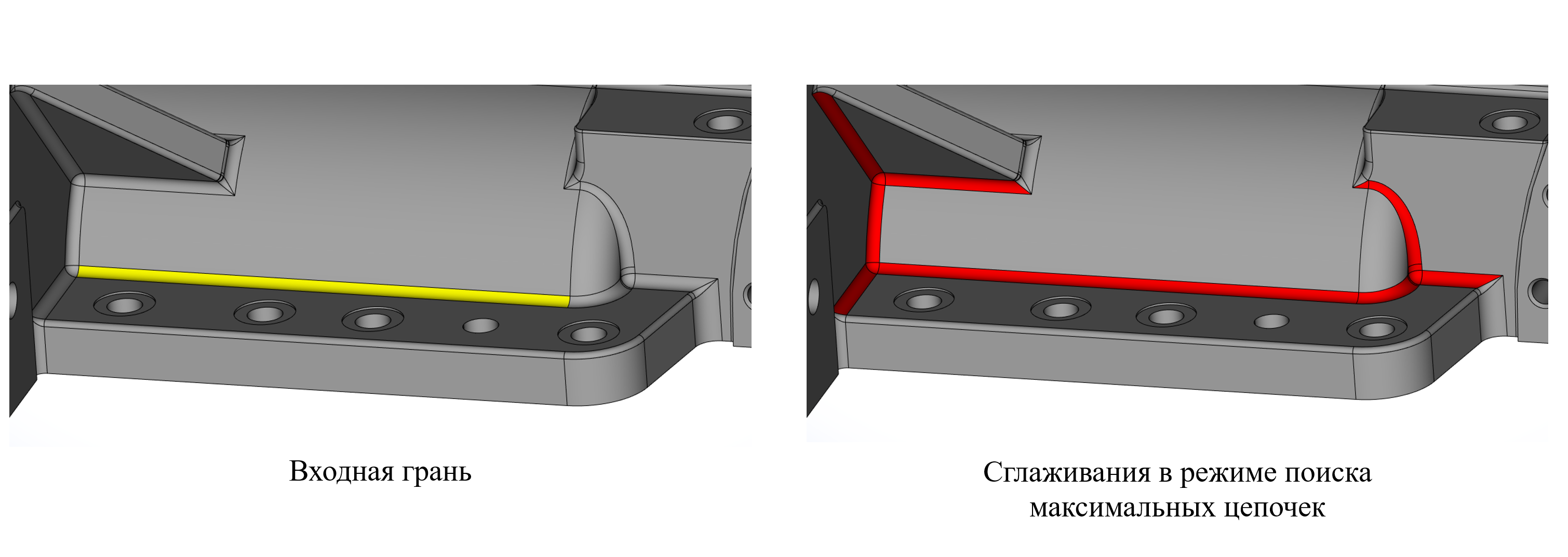
Распознавание цепочки сглаживаний постоянного радиуса
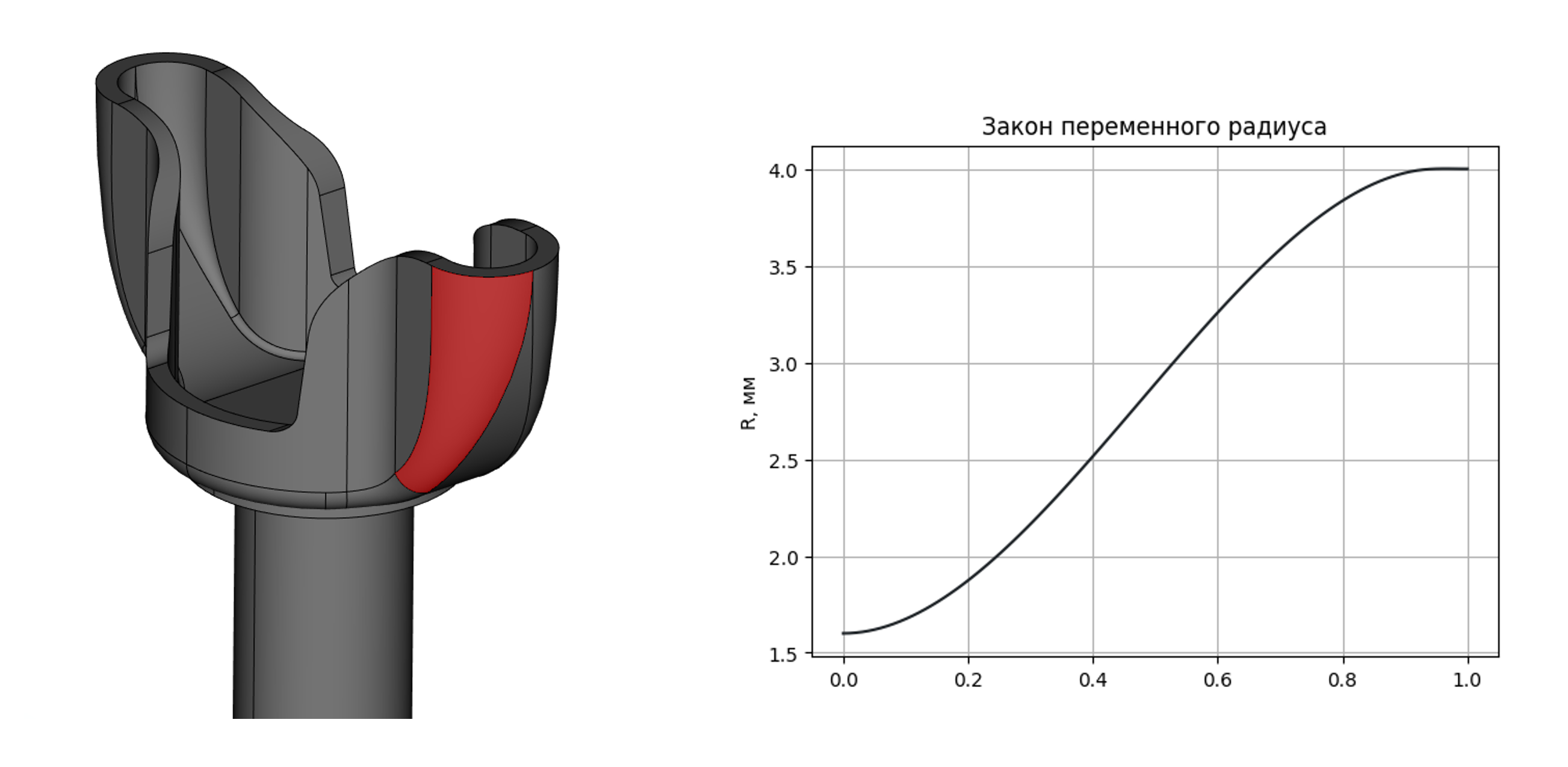
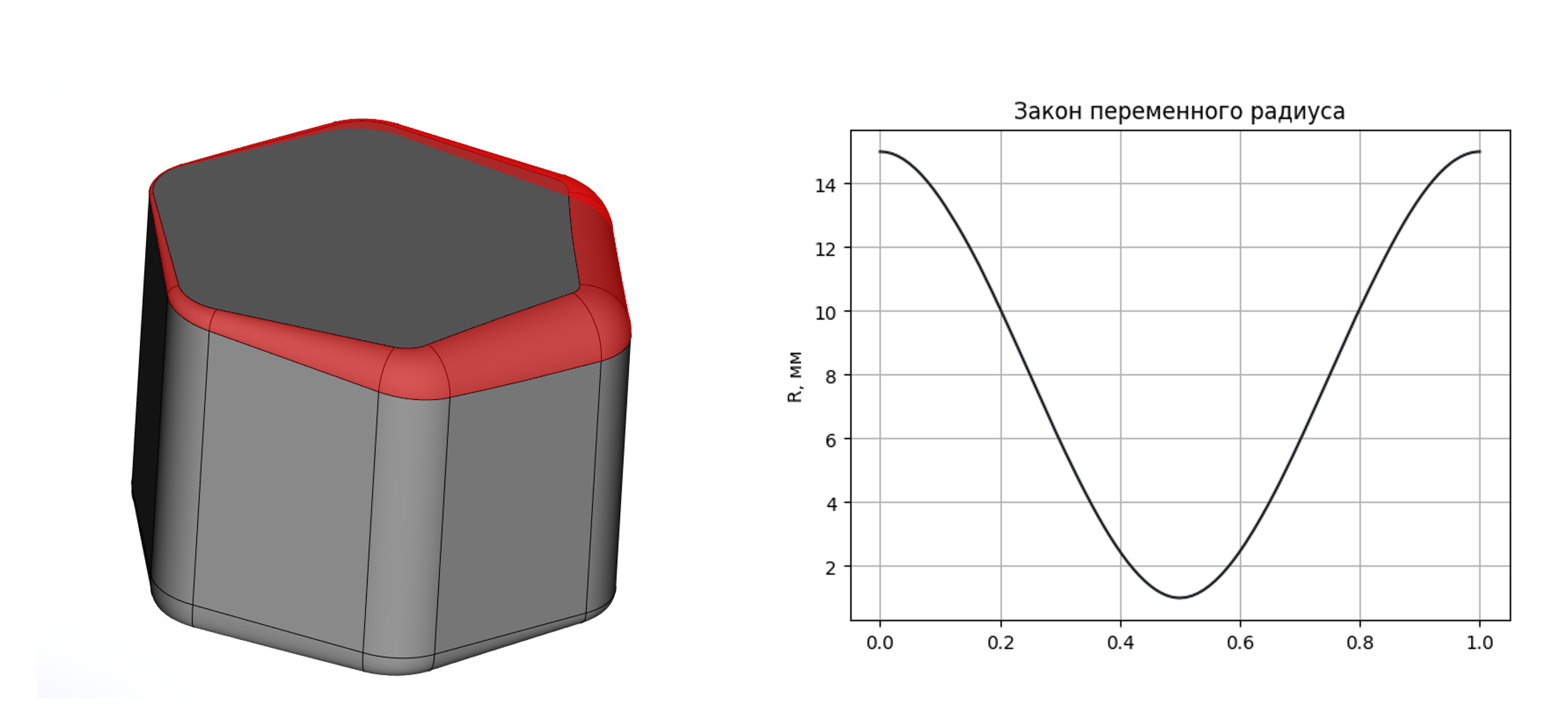
Распознавание закона переменного радиуса на импортированной модели
В ядре реализована функциональность перестроения распознанных сглаживаний с новыми радиусами, в том числе и с изменением типа сглаживания (например, постоянный радиус можно заменить на переменный).
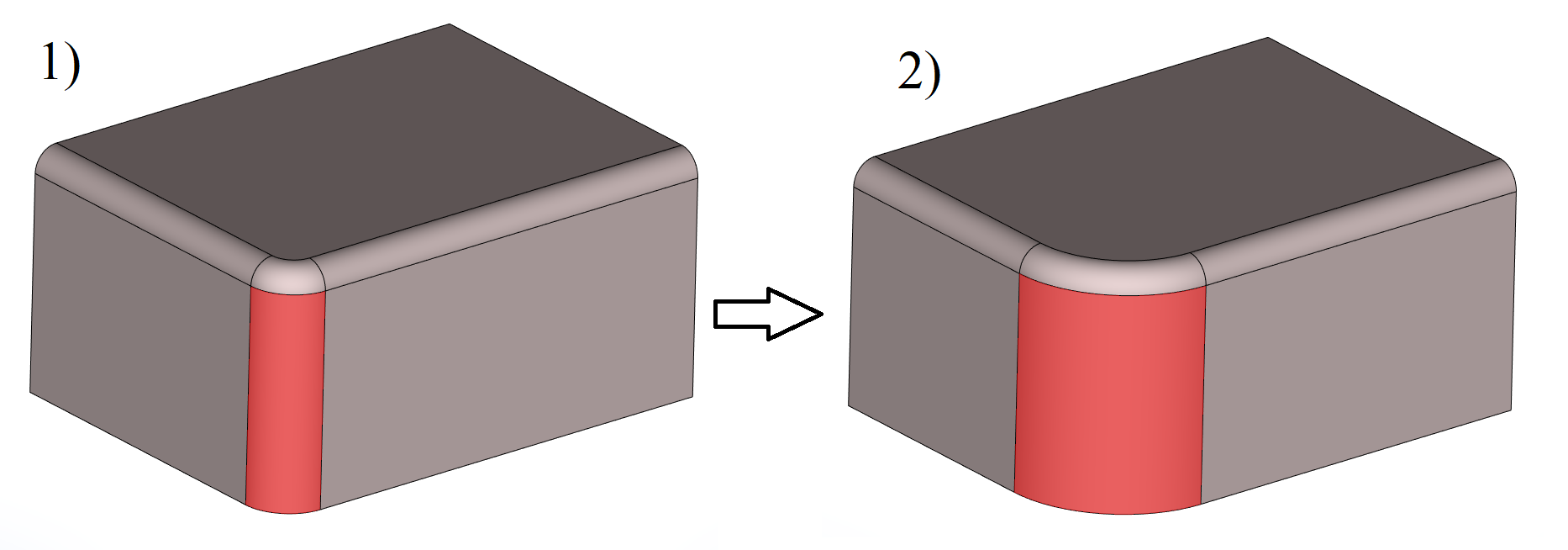
Изменение распознанного сглаживания постоянного радиуса
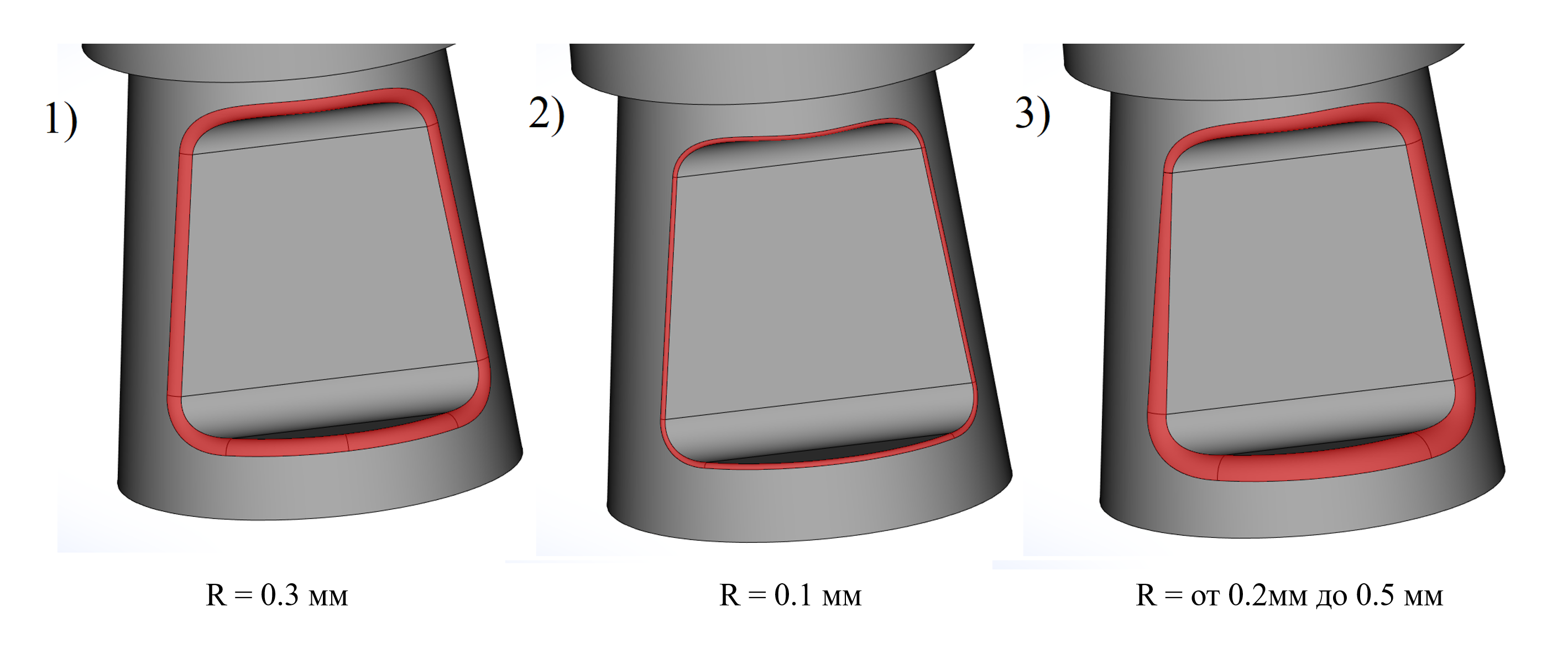
Изменение радиуса у импортированных сглаживаний (1 – распознанное сглаживание; 2- перестроенное сглаживание постоянного радиуса; 3 – перестроенное сглаживание переменного радиуса)
Функциональность распознавания и перестроения сглаживаний поддерживается теперь и в операции копирования граней по образцу («паттернинга»).
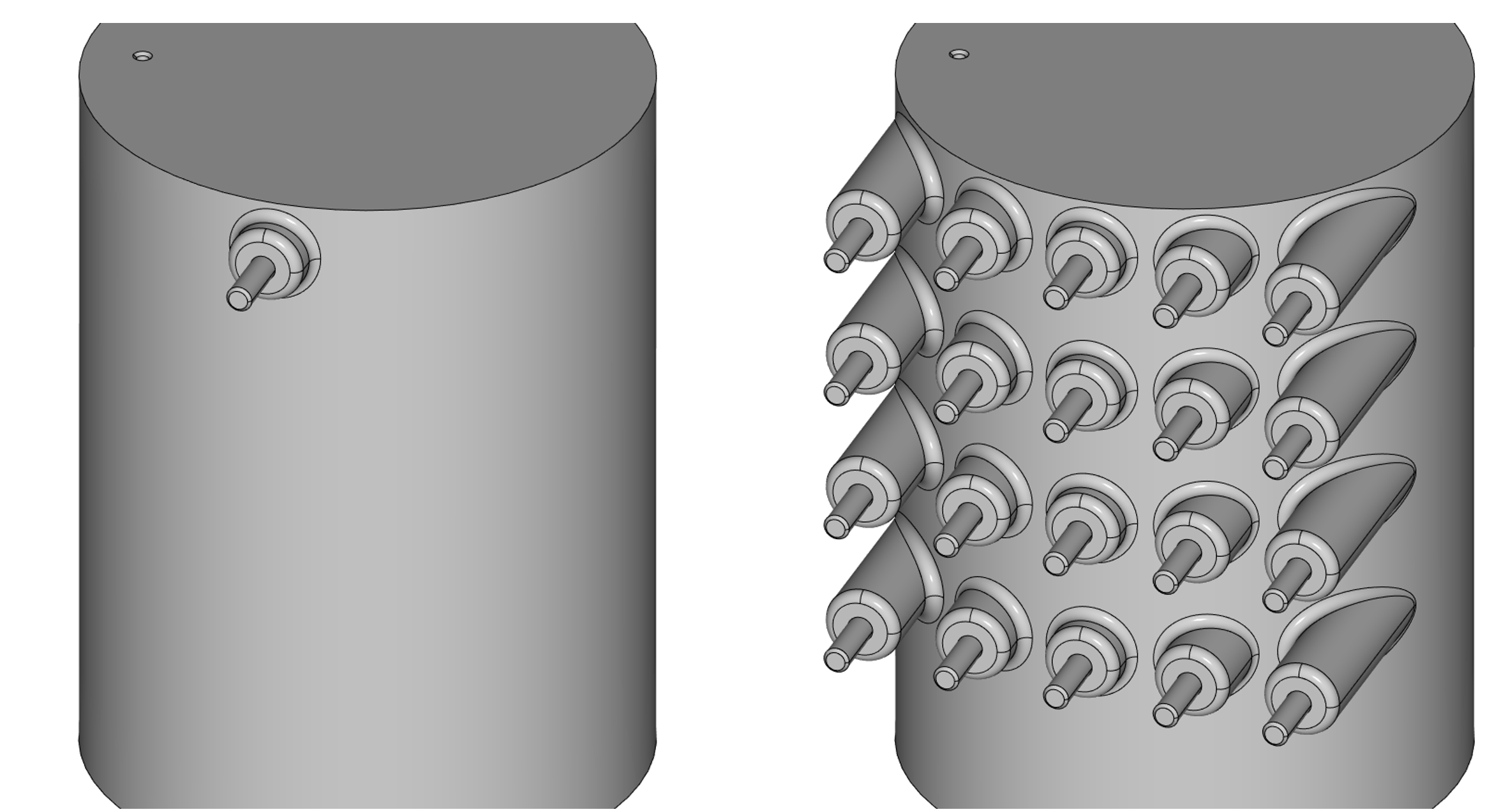
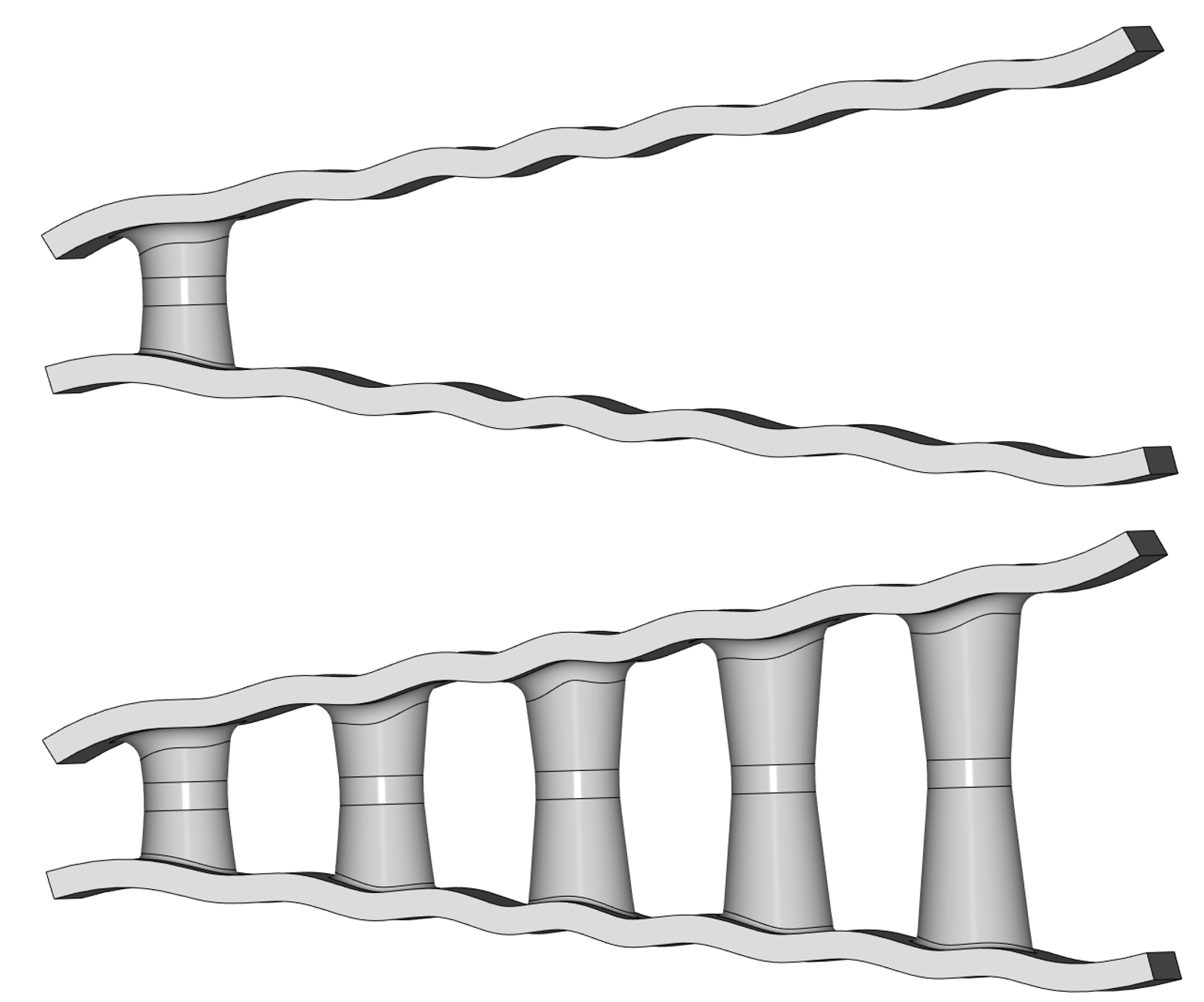
Примеры копирования граней с автоматической адаптацией размеров и сглаживаний у основания
Помимо этого, доработана сама схема копирования граней, снят ряд важных ограничений операции.
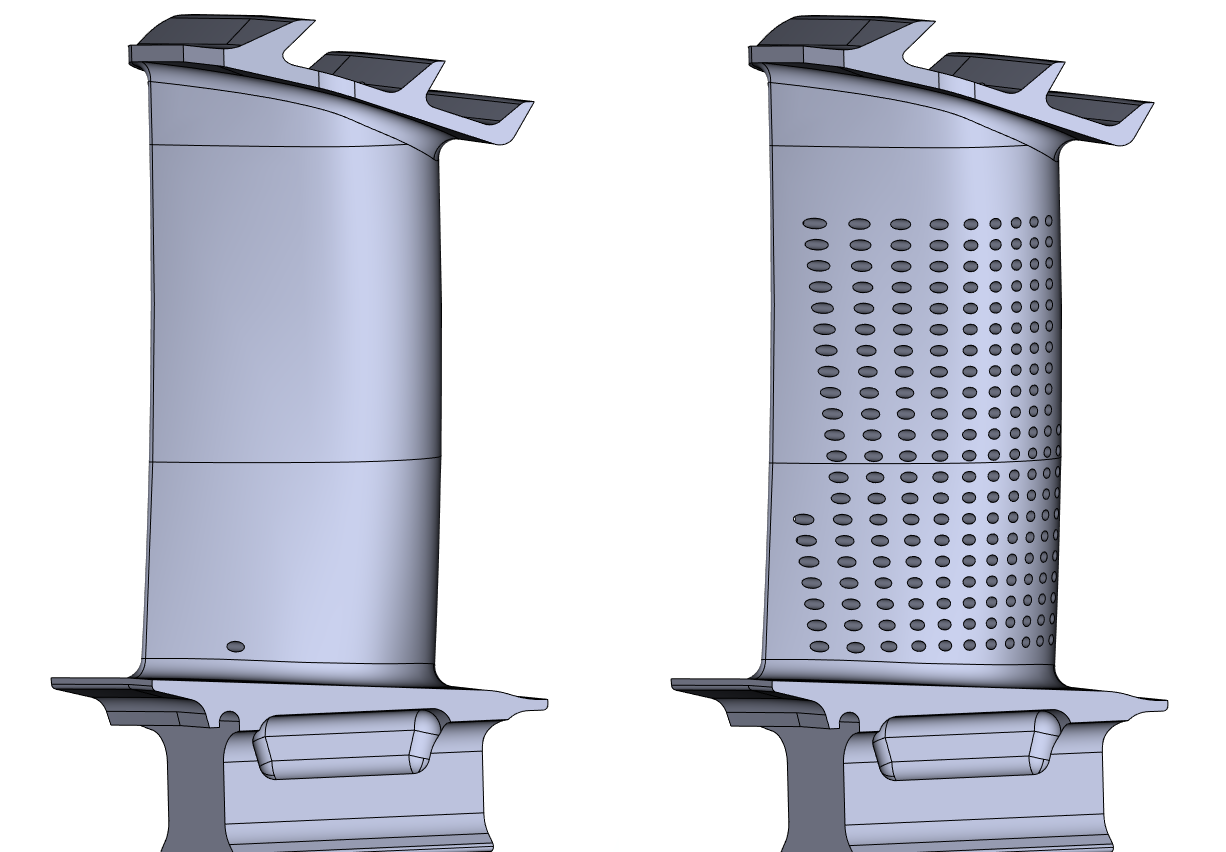
Пример размножения отверстия вдоль сложной поверхности
В операцию «по траектории» было добавлено большое число новых режимов и обработок специальных конфигураций. В частности, теперь поддерживается многопрофильный свип – возможность использовать несколько разных по геометрии и топологии профилей с одной траекторией. Эта функциональность значительно расширяет возможности моделирования сложной геометрии.
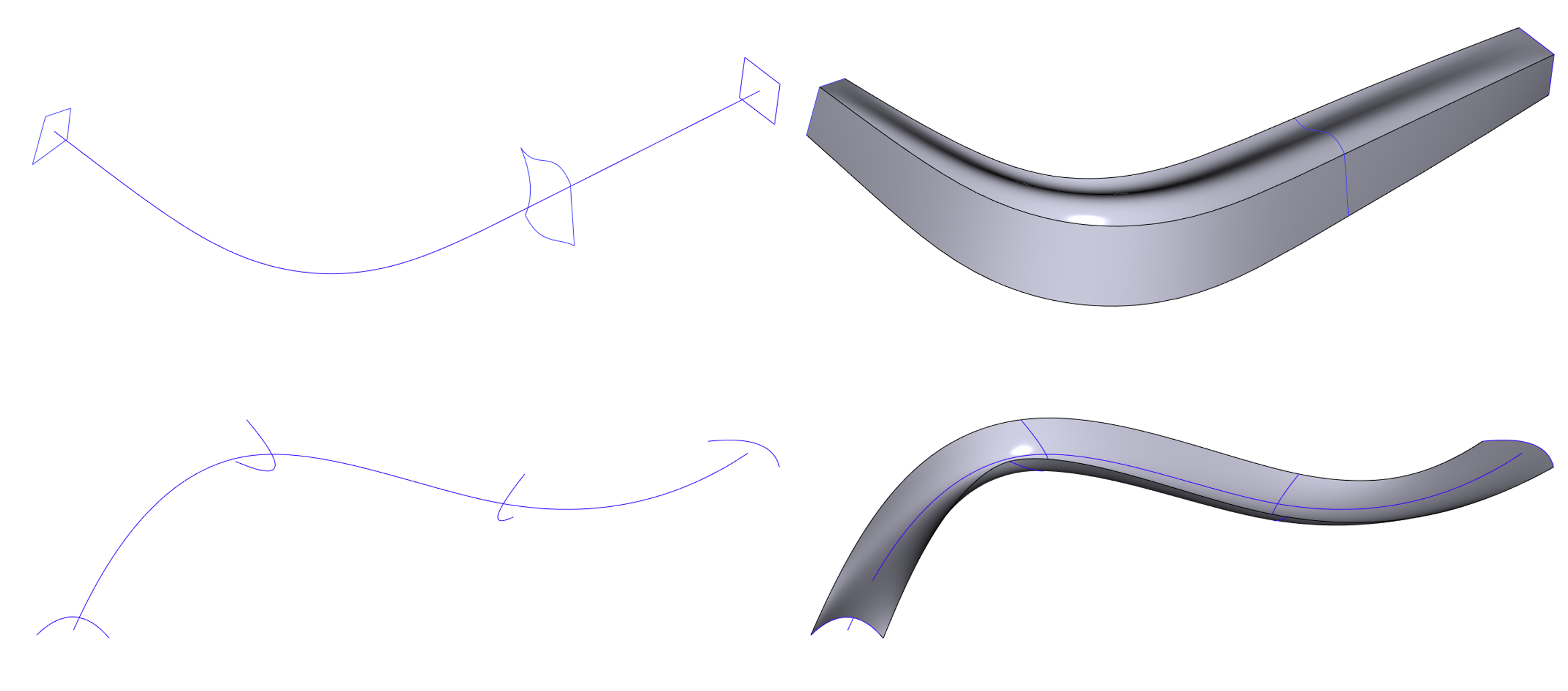
Пример многопрофильного свипа с получением как твёрдого, так и листового тела
Следует отметить, что при использовании нескольких профилей поддерживается как задание дополнительных законов кручения и масштабирования, так и задание соответствия вершин профилей между собой. Ещё одной интересной возможностью является поддержка в качестве начального или конечного профиля разомкнутого проволочного тела, при том что все остальные профили замкнуты, и в итоге строится твёрдое тело, а не поверхность. Благодаря такой возможности можно построить тело типа «тюбик».
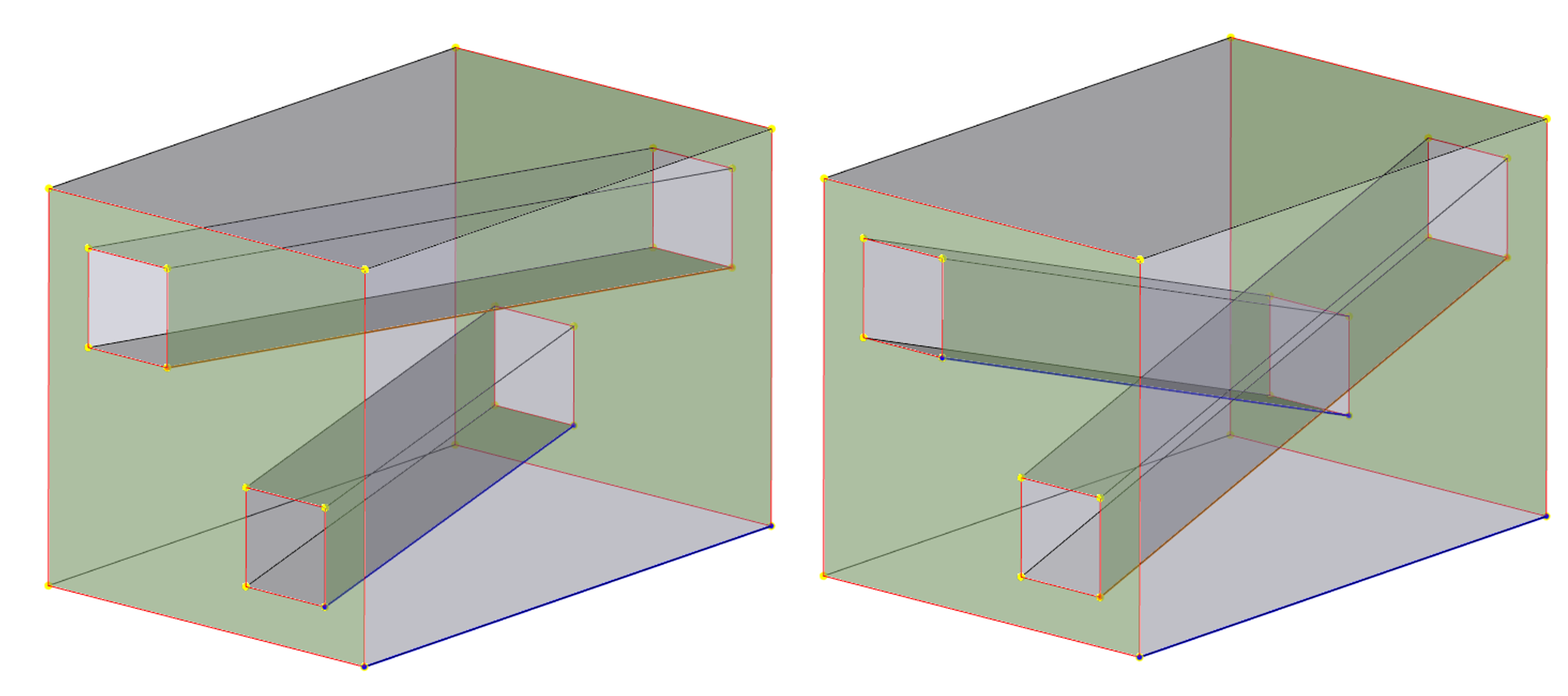
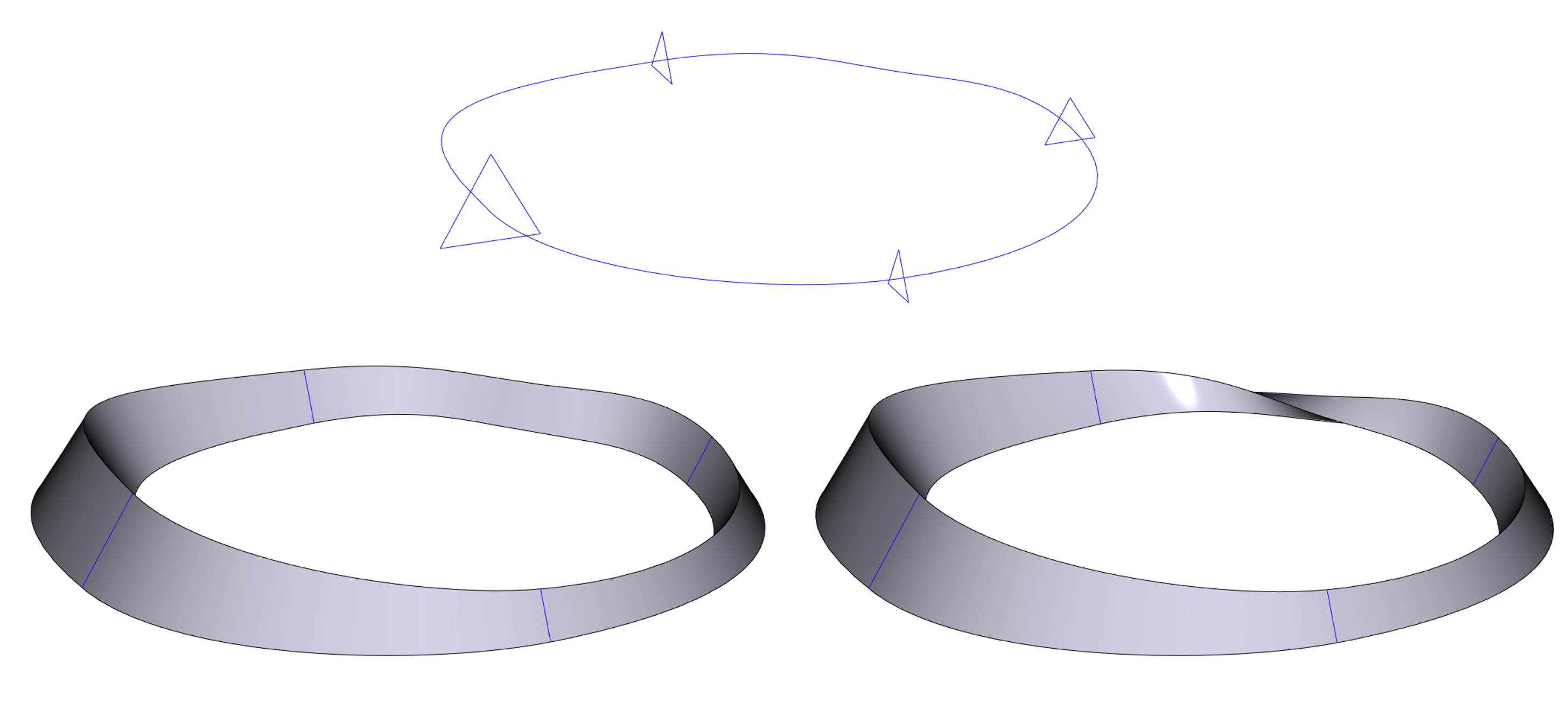
Задание соответствия вершин в многопрофильном свипе
Добавлена поддержка разных режимов законов масштабирования профиля. Причём все эти режимы можно комбинировать с законами кручения.
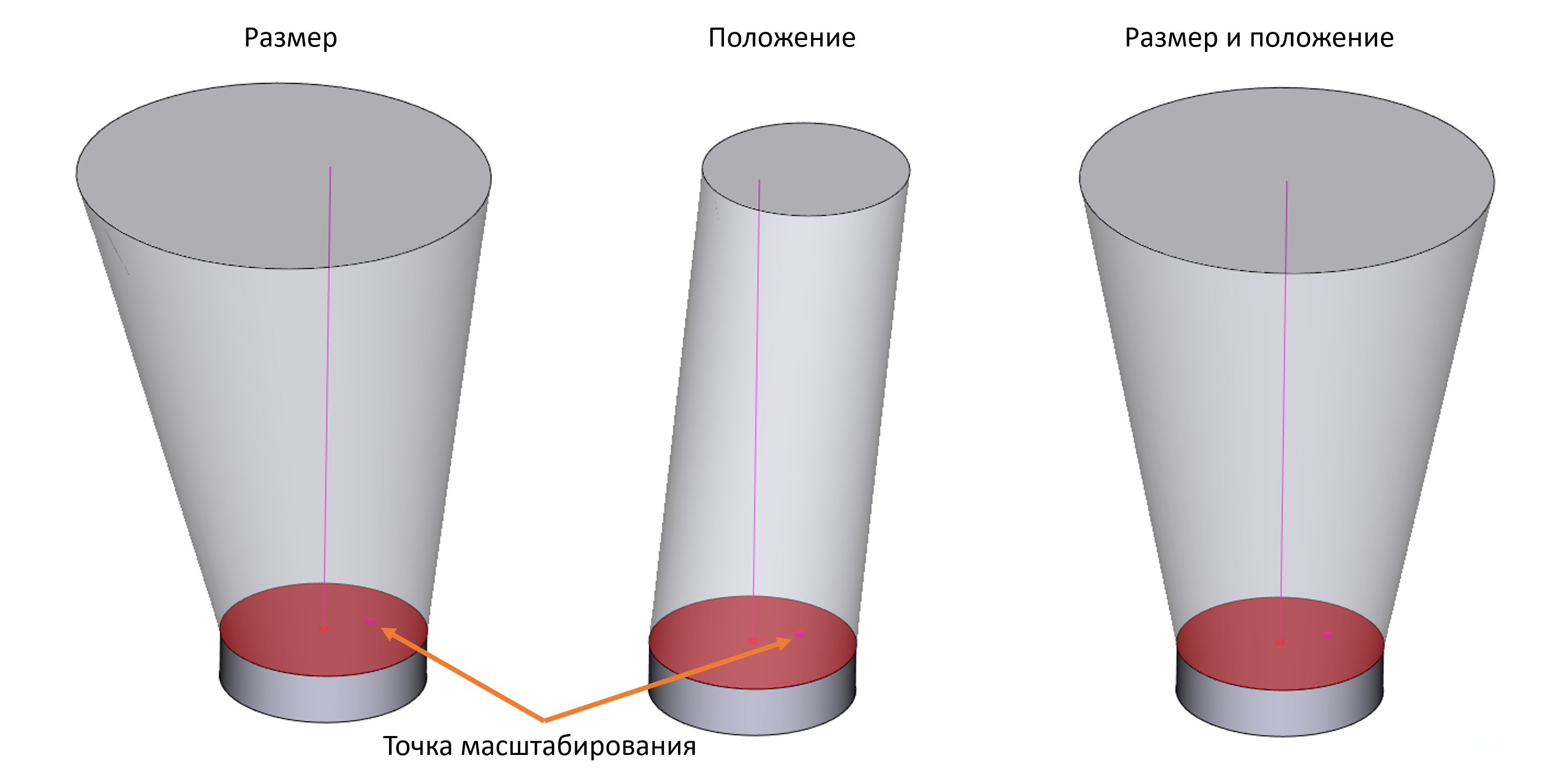
Опции законов масштабирования в свипе
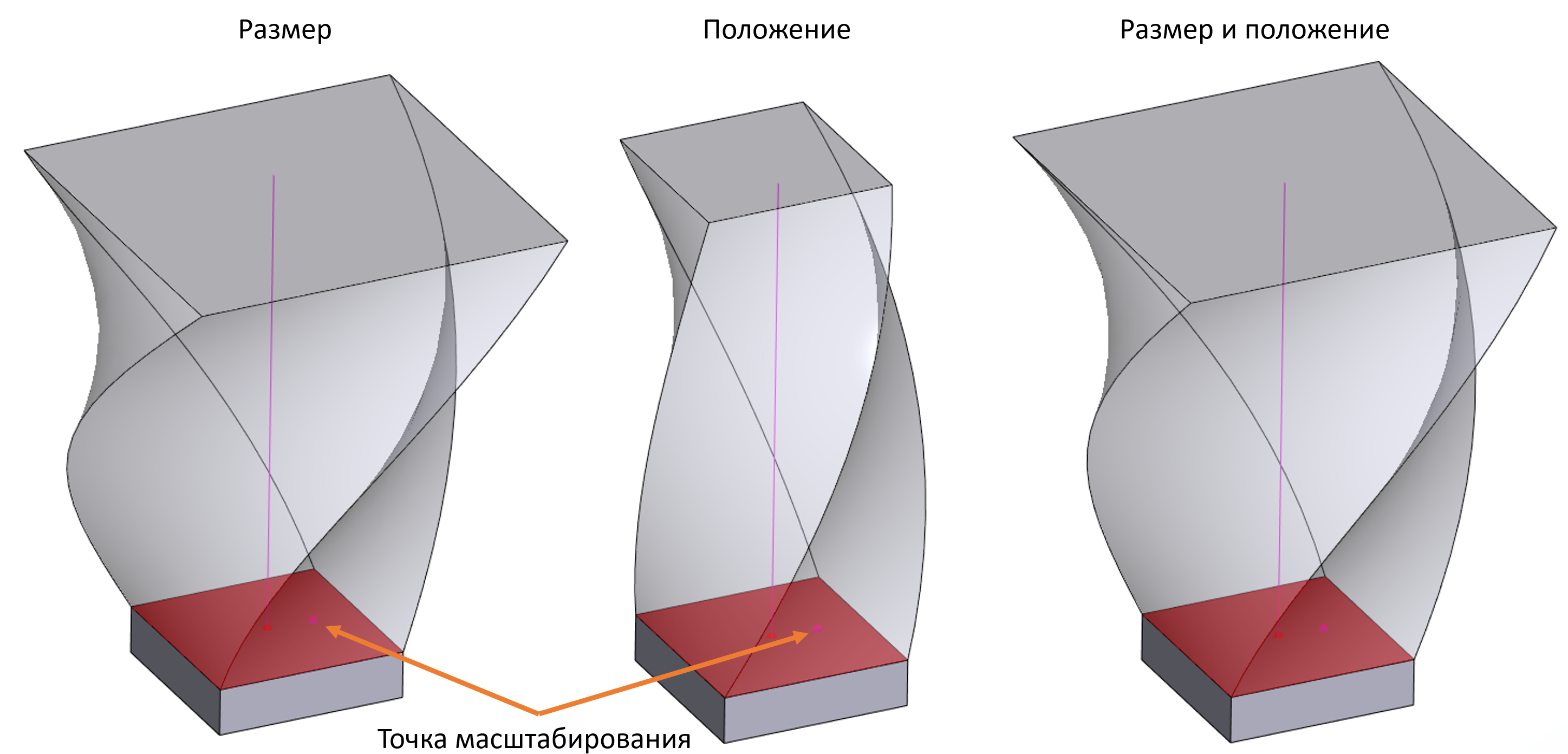
Комбинация закона масштабирования и закона кручения
Одной интересной особенностью масштабирования в новой версии RGK является поддержка нулевого масштаба в начале или конце траектории, когда профиль «схлопывается» в вершину.
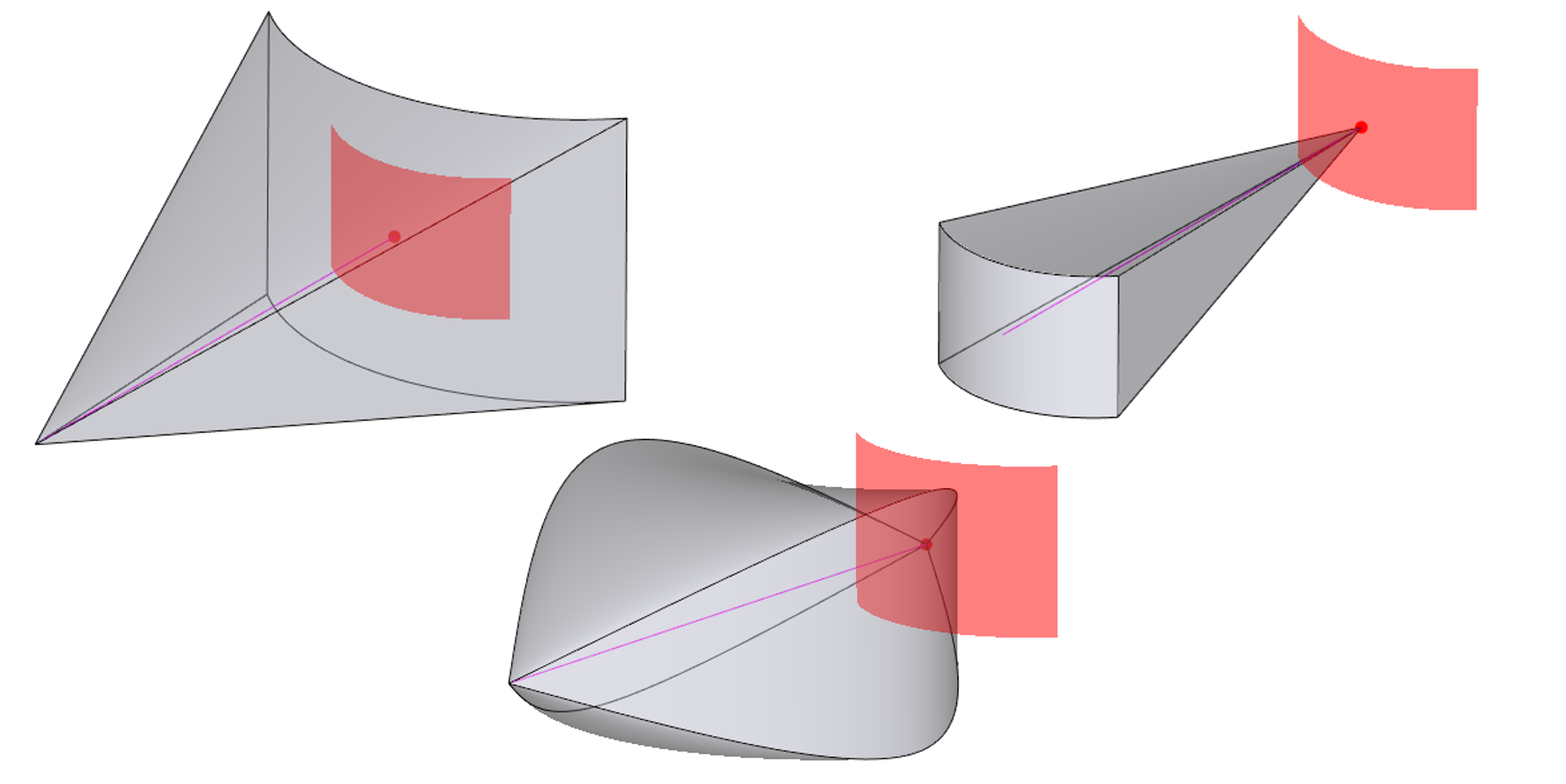
Пример поддержки нулевого масштаба в свипе
Улучшена обработка изломов траектории с формированием скруглённых зон на поверхности тела
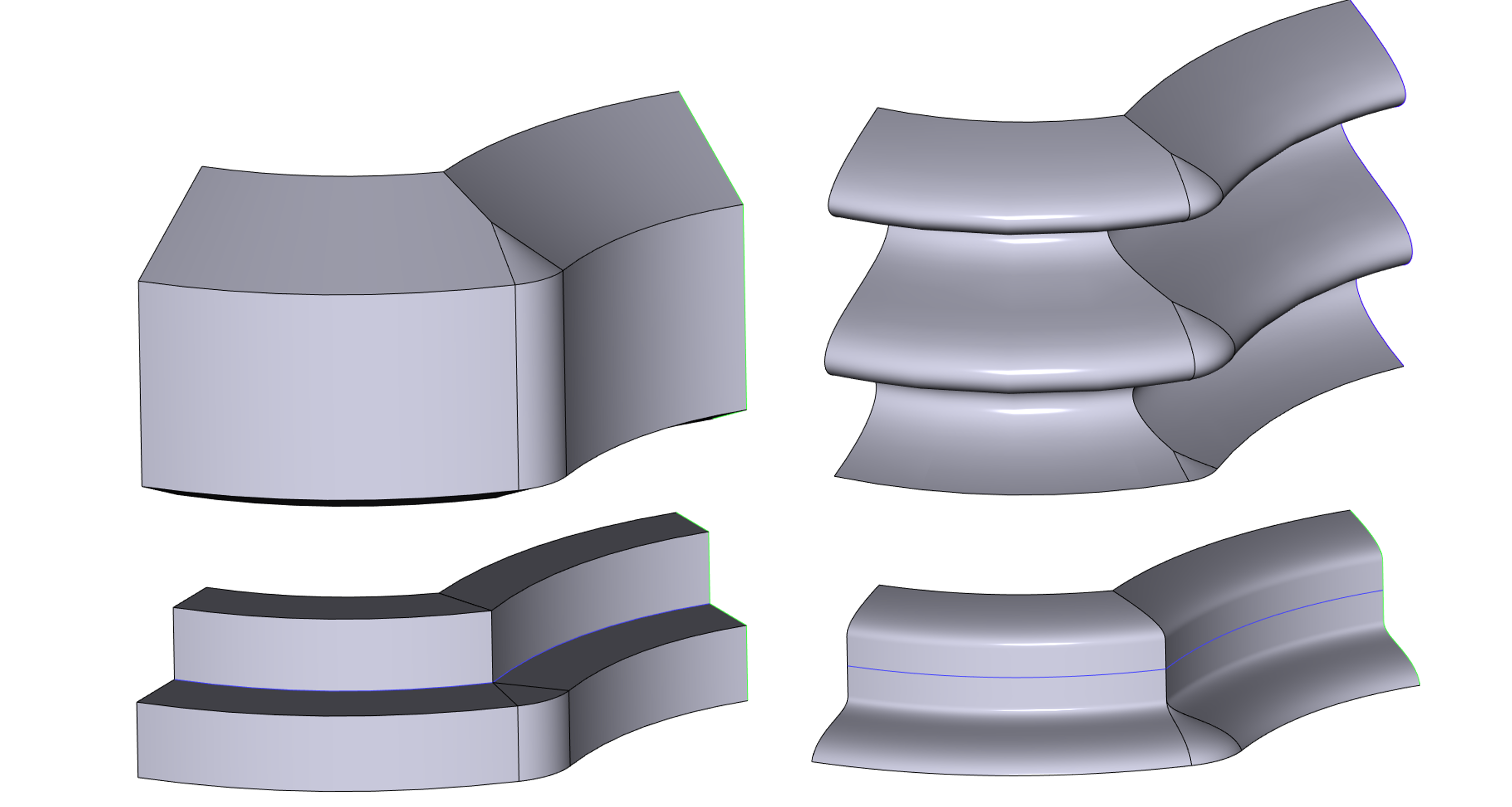
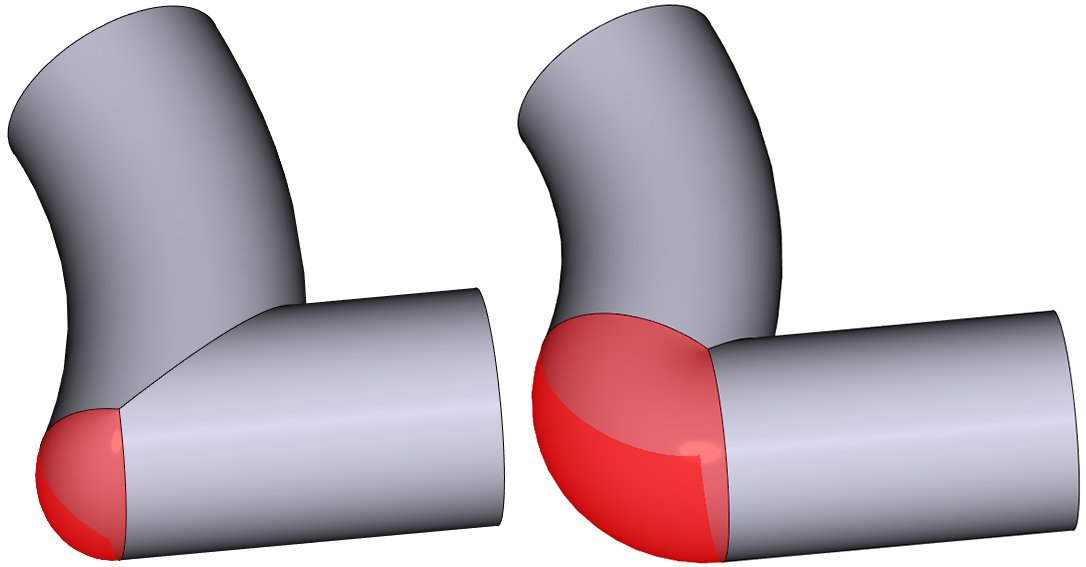
Примеры обработки углов траектории в новой версии RGK
В свипе с несколькими траекториями выполнены важные доработки по синхронизации траектории и направляющих, а также реализована поддержка G1 разрывных направляющих.
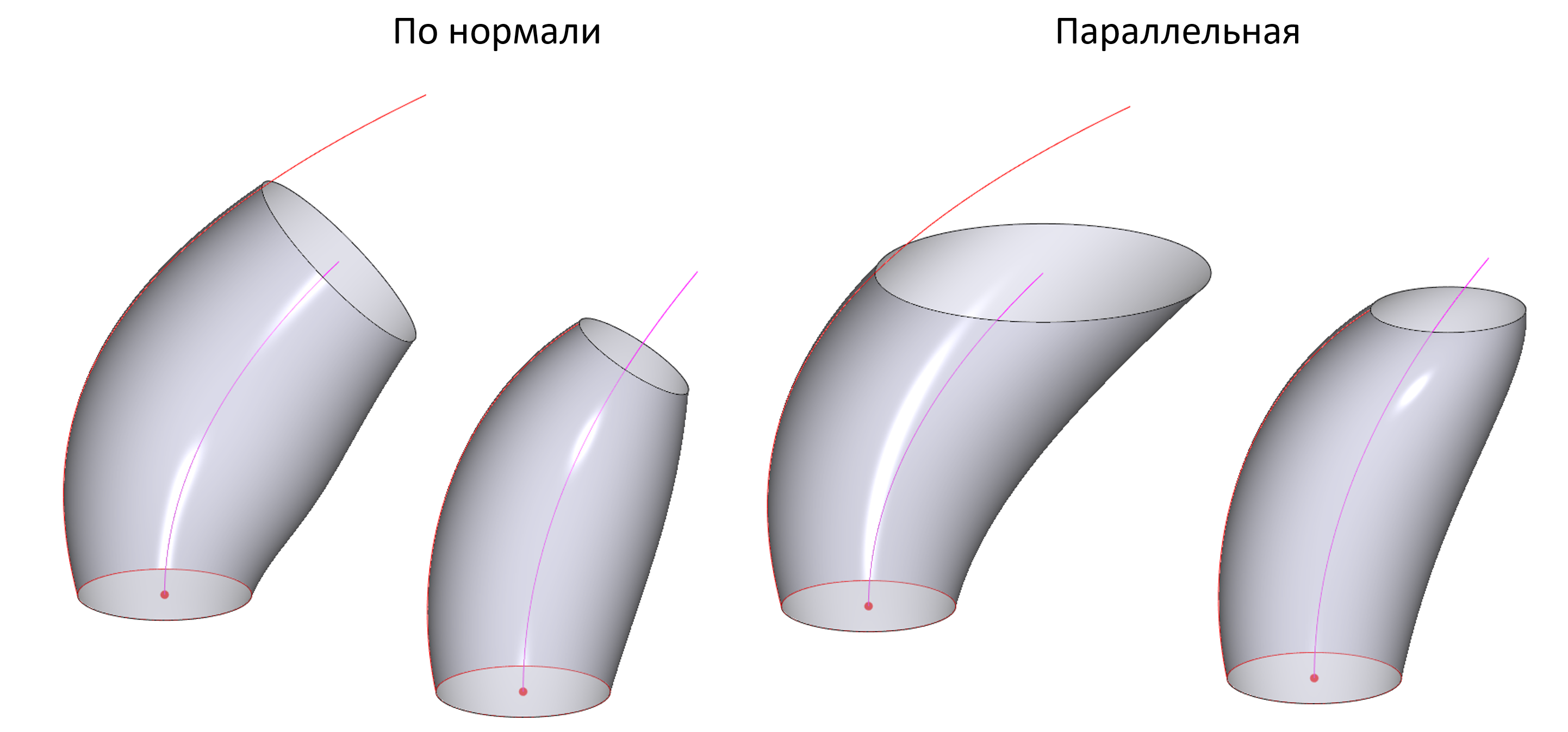
Режимы синхронизации траектории и направляющих
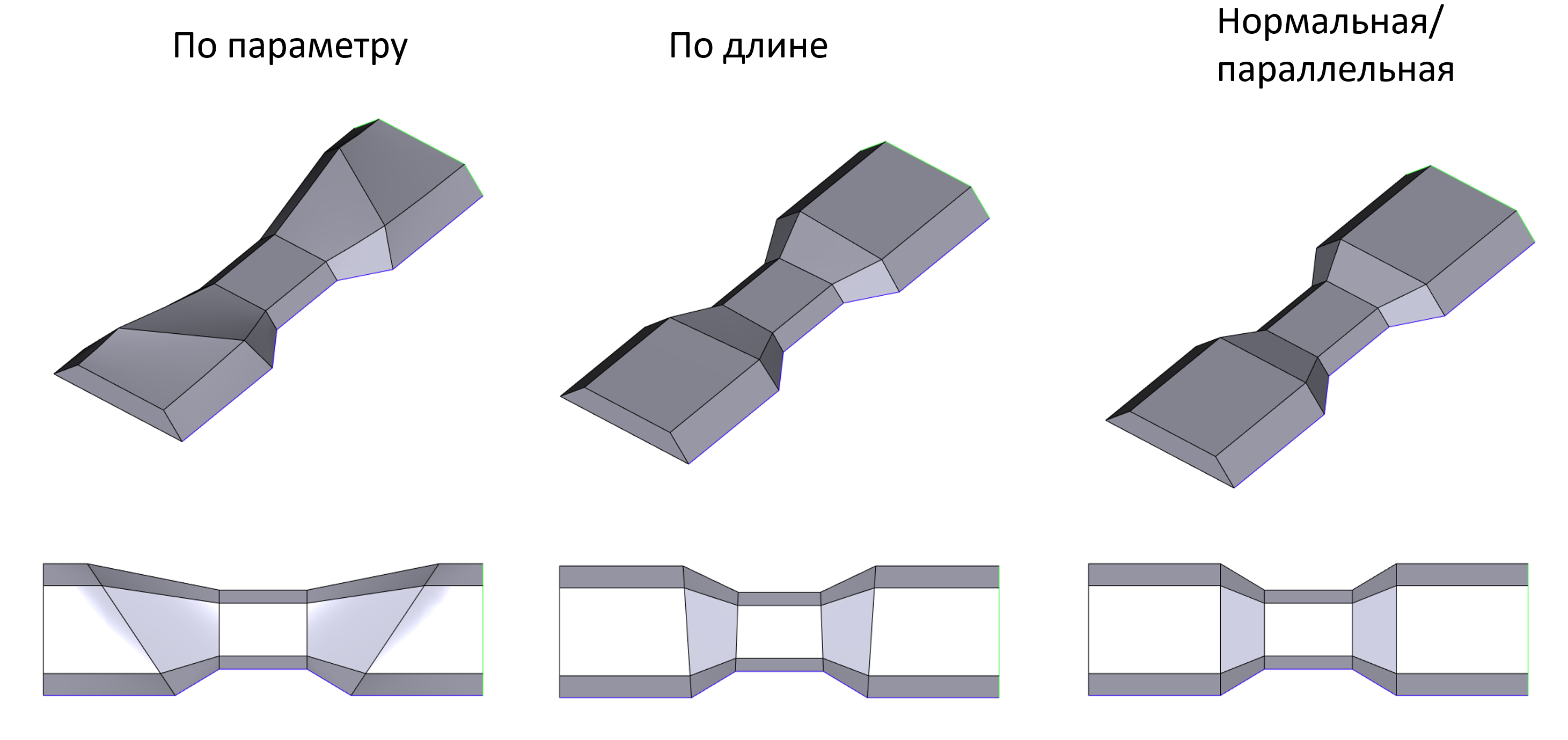
Поддержка G1 разрывных направляющих и эффект от применения разных законов синхронизации
В новой версии ядра расширилась функциональность построения уклонов граней тела. Во-первых, реализована поддержка нескольких новых типов поверхностей уклона. Теперь в RGK поддерживаются следующие типы поверхностей:
- Isocline (используется по умолчанию) – сохраняет угол между направлением уклона и нормалью к поверхности уклона
- Surface – направляющая определяется направлением уклона и нормалью к исходной поверхности
- Curve – направляющая определяется направлением уклона и касательной к исходной кривой
- Normal – направление уклона определяется нормалью к прилежащей поверхности
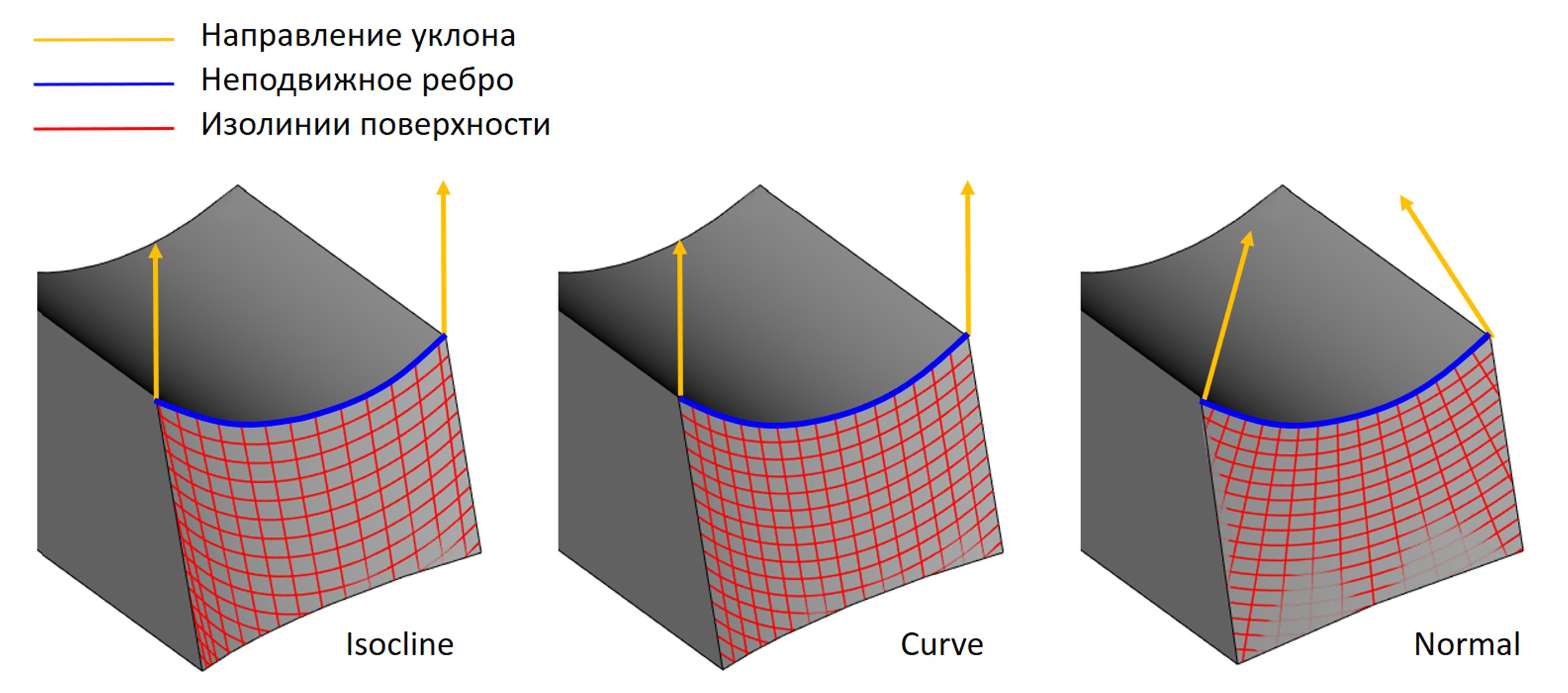
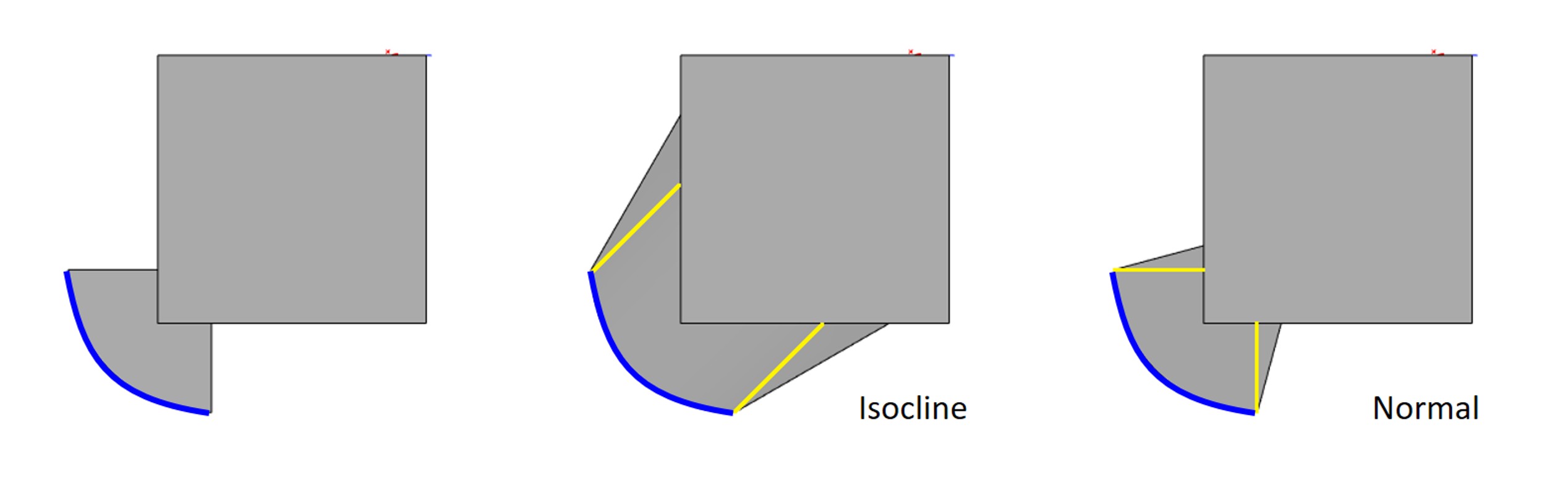
Иллюстрация отличий поверхностей уклона
Во-вторых, добавлены важные на практике топологические обработки, повышающие надёжность алгоритма. В частности, поддержка инверсии граней при необходимости.
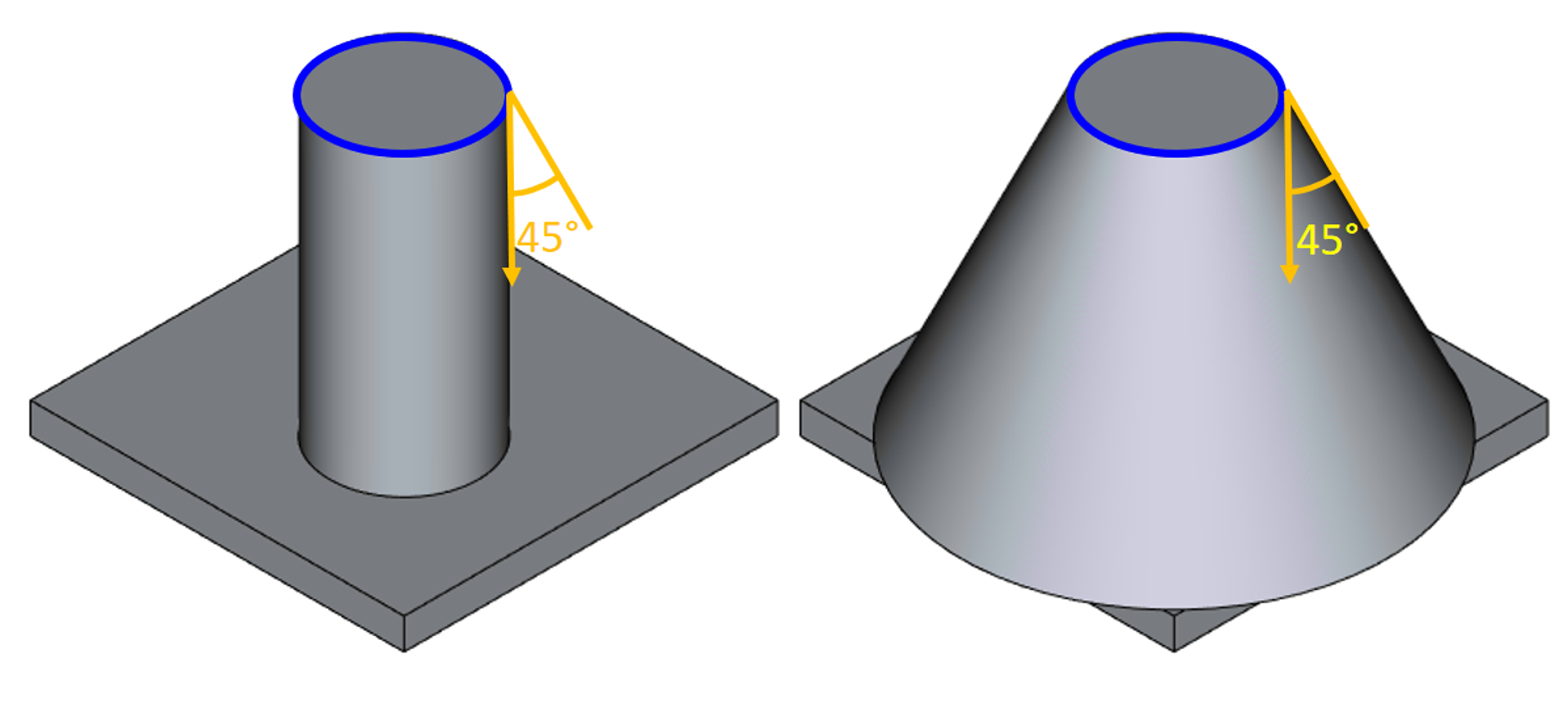
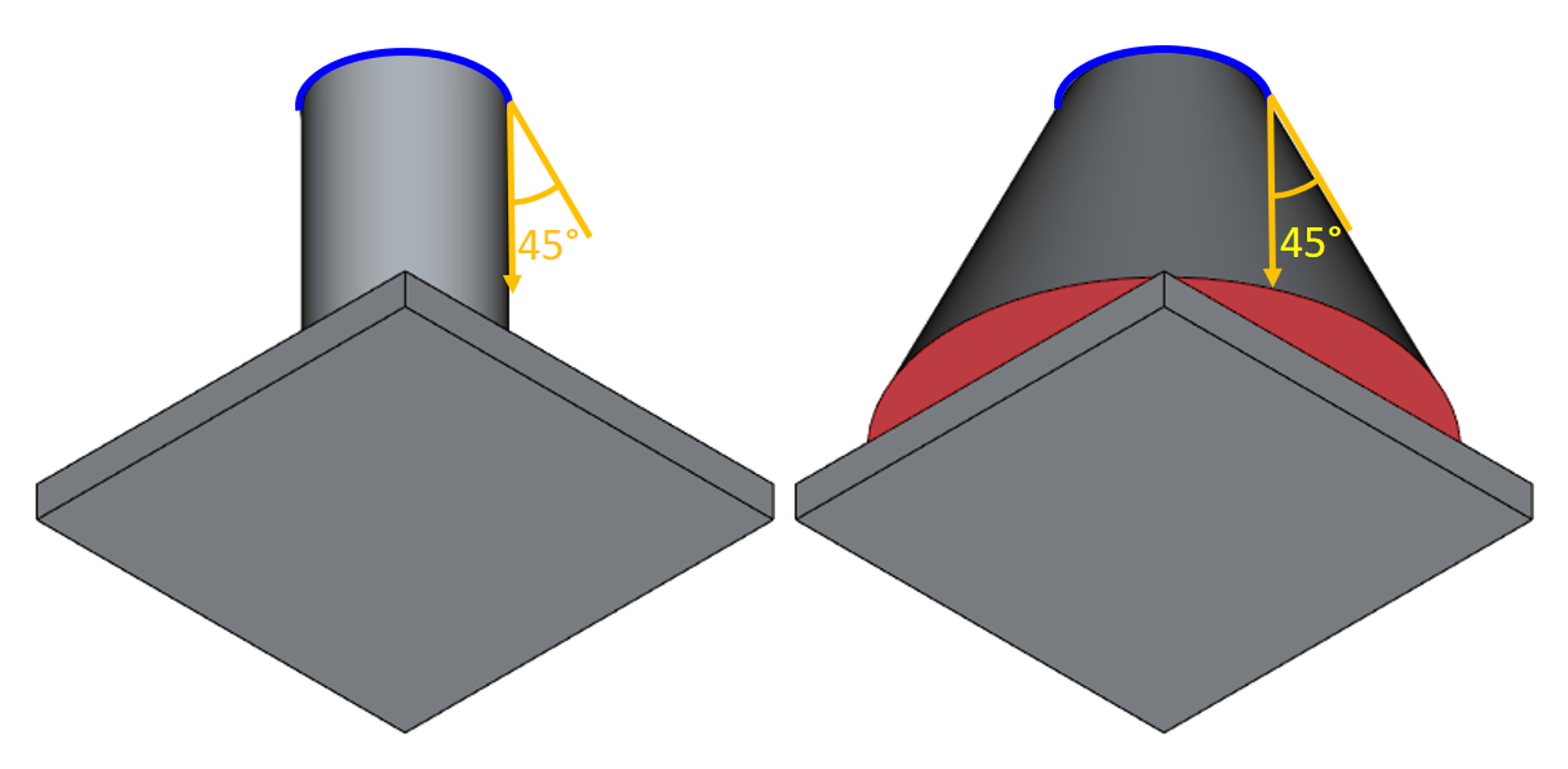
Инверсия граней при выходе уклона за пределы базовой топологии
Реализована поддержка составных линий разъёма и разбиения уклоняемой грани, содержащей несколько фиксированных рёбер.
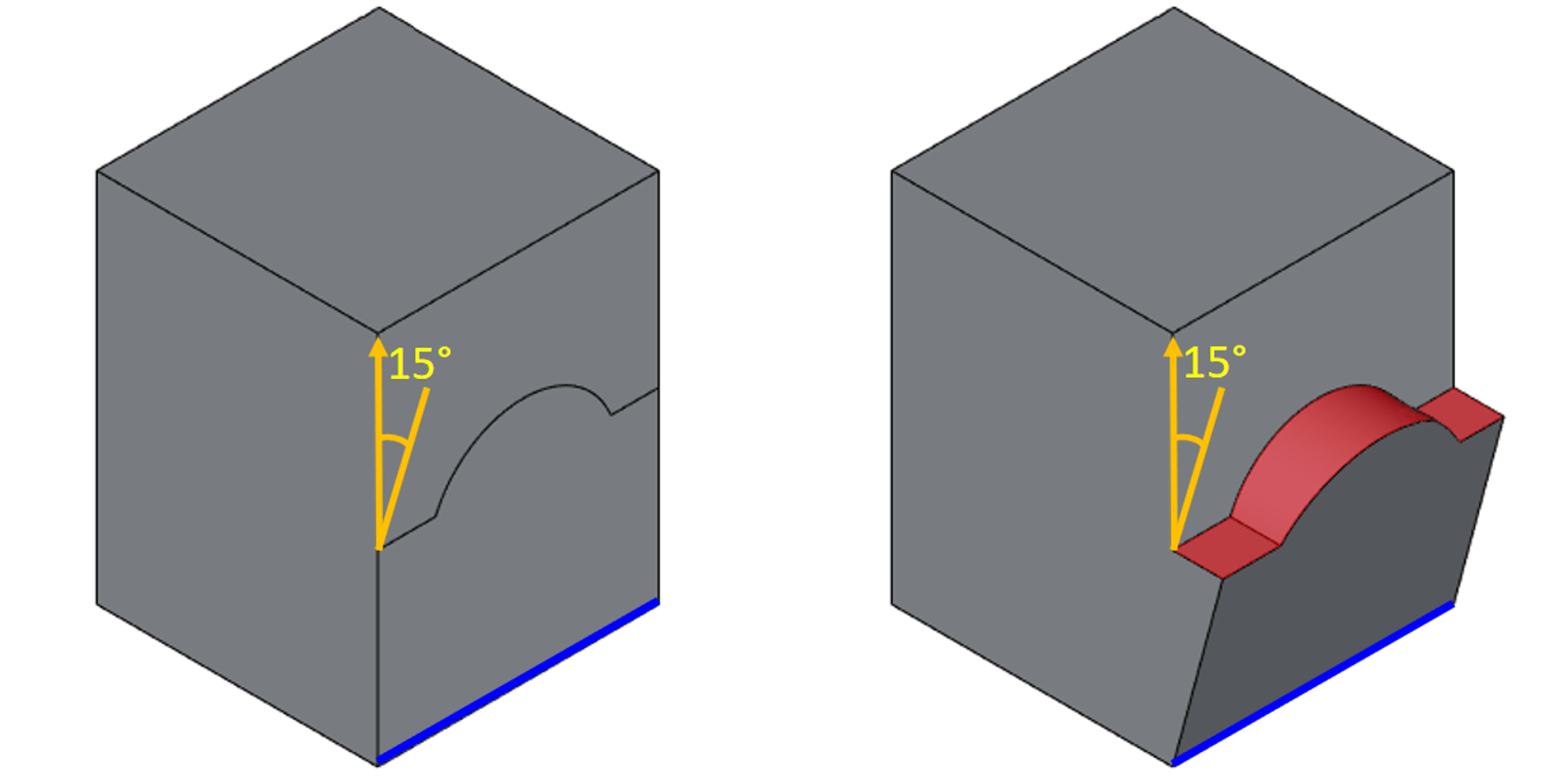
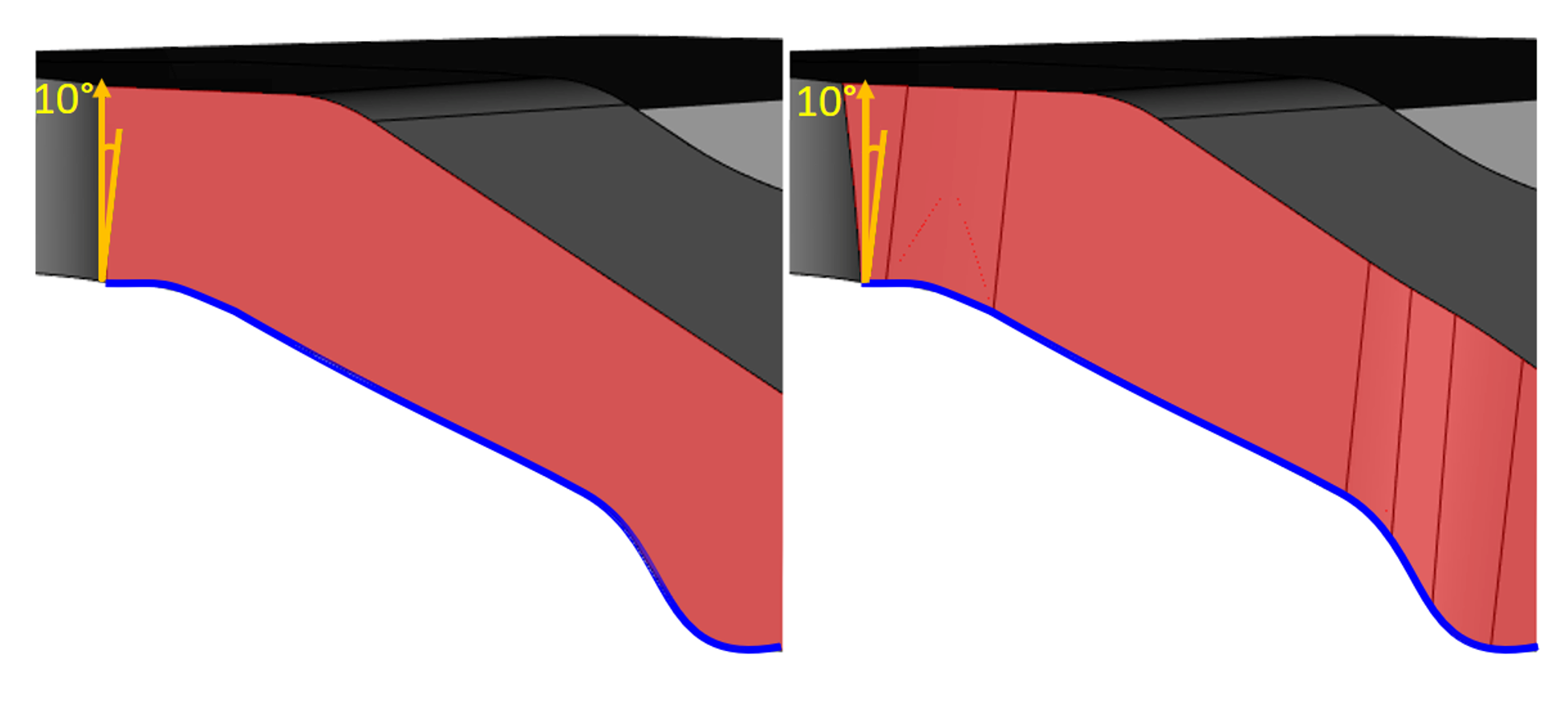
Иллюстрация топологических обработок в новой версии операции «Уклон» RGK
Следует отдельно отметить, что RGK позволяет за одну операцию строить уклоны с разными углами для разных граней.
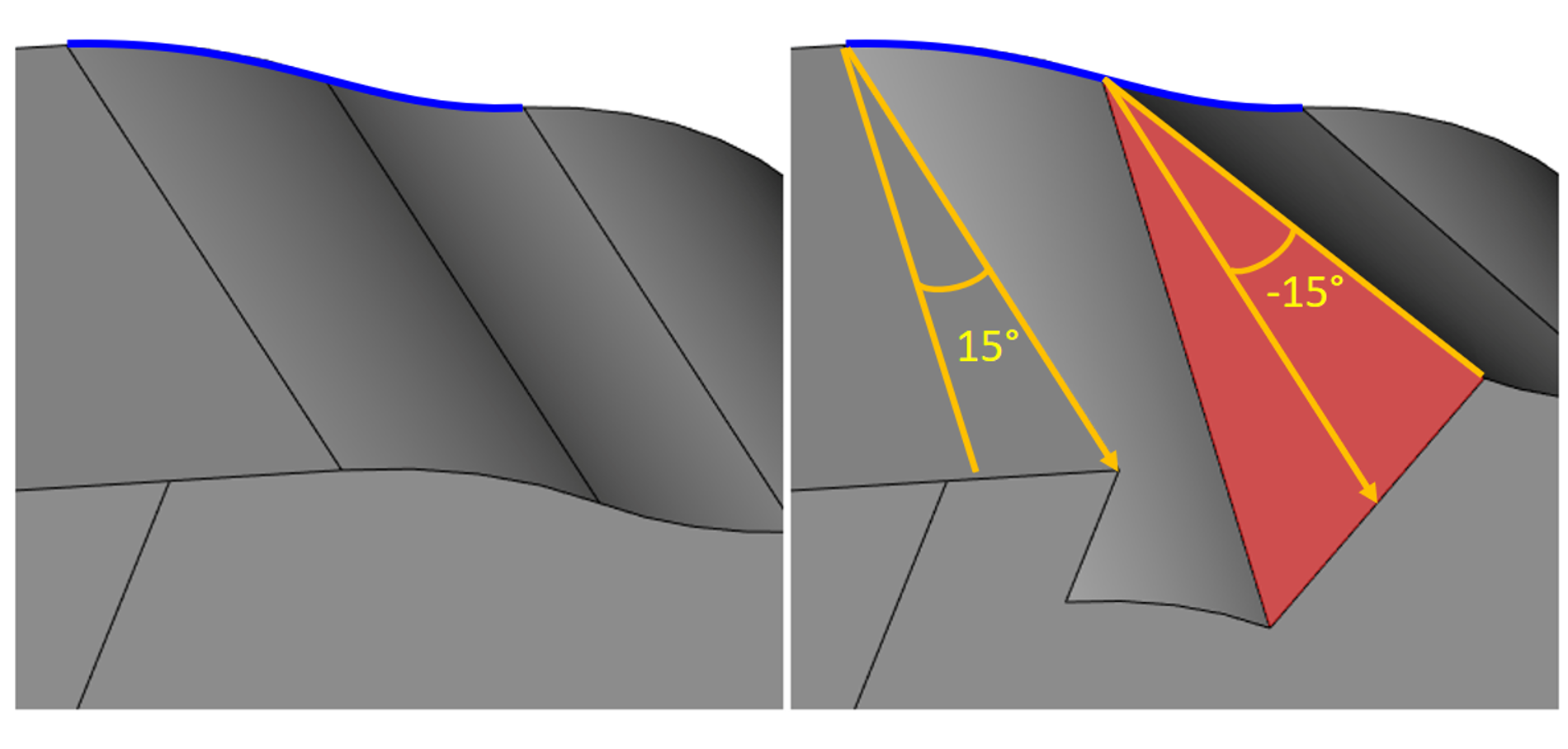
Пример уклонения двух изначально гладко состыкованных граней на разные углы
Дальнейшее развитие получили возможности ядра по построению уклонов с заданными поверхностями разъёма. Как практически везде под «поверхностью» понимается листовое тело – набор связанных, согласованно ориентированных граней без свойства замыкания объёма. Было убрано ограничение на использование только одной грани как поверхности разъёма.
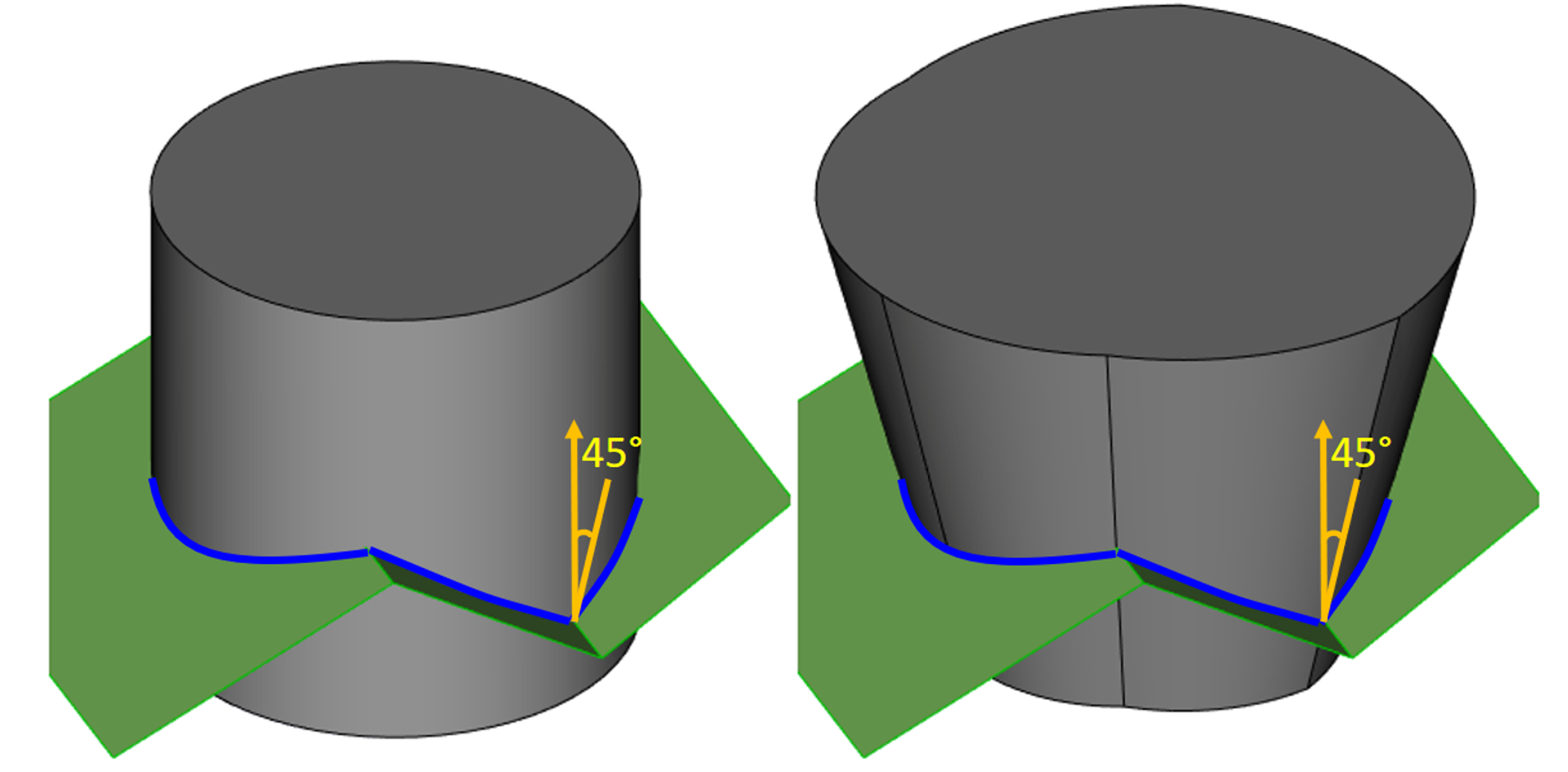
Иллюстрация работы с многогранной поверхностью разъёма
Напомним, что уклоны, как и многие «локальные» операции в RGK, могут работать в «глобальном» режиме, когда, при необходимости, модификации подвергаются не только соседние грани тела, но и отстоящие от них. В новой версии эта возможность получила дальнейшее развитие за счёт усовершенствования многих базовых инструментальных алгоритмов ядра.
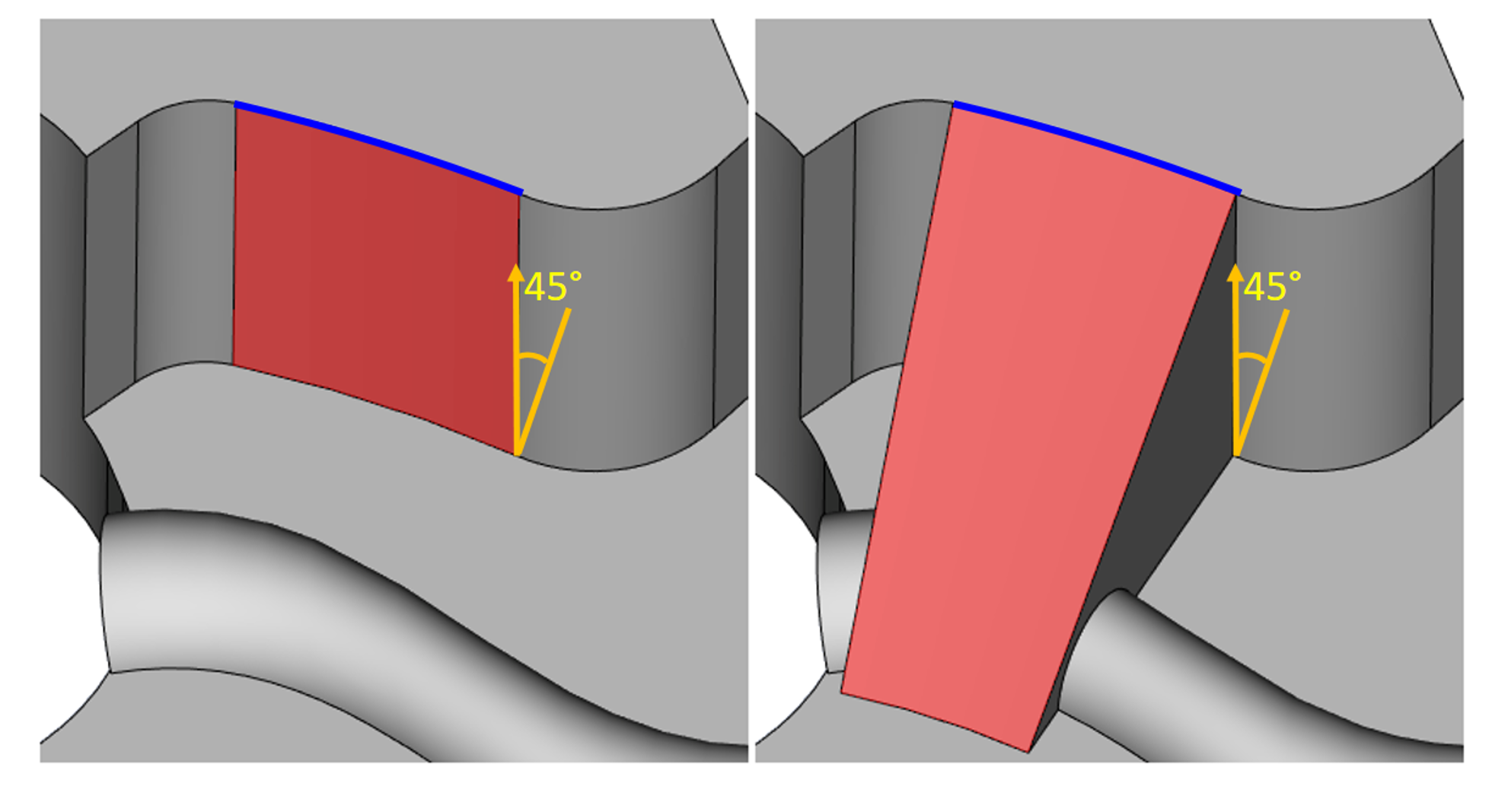
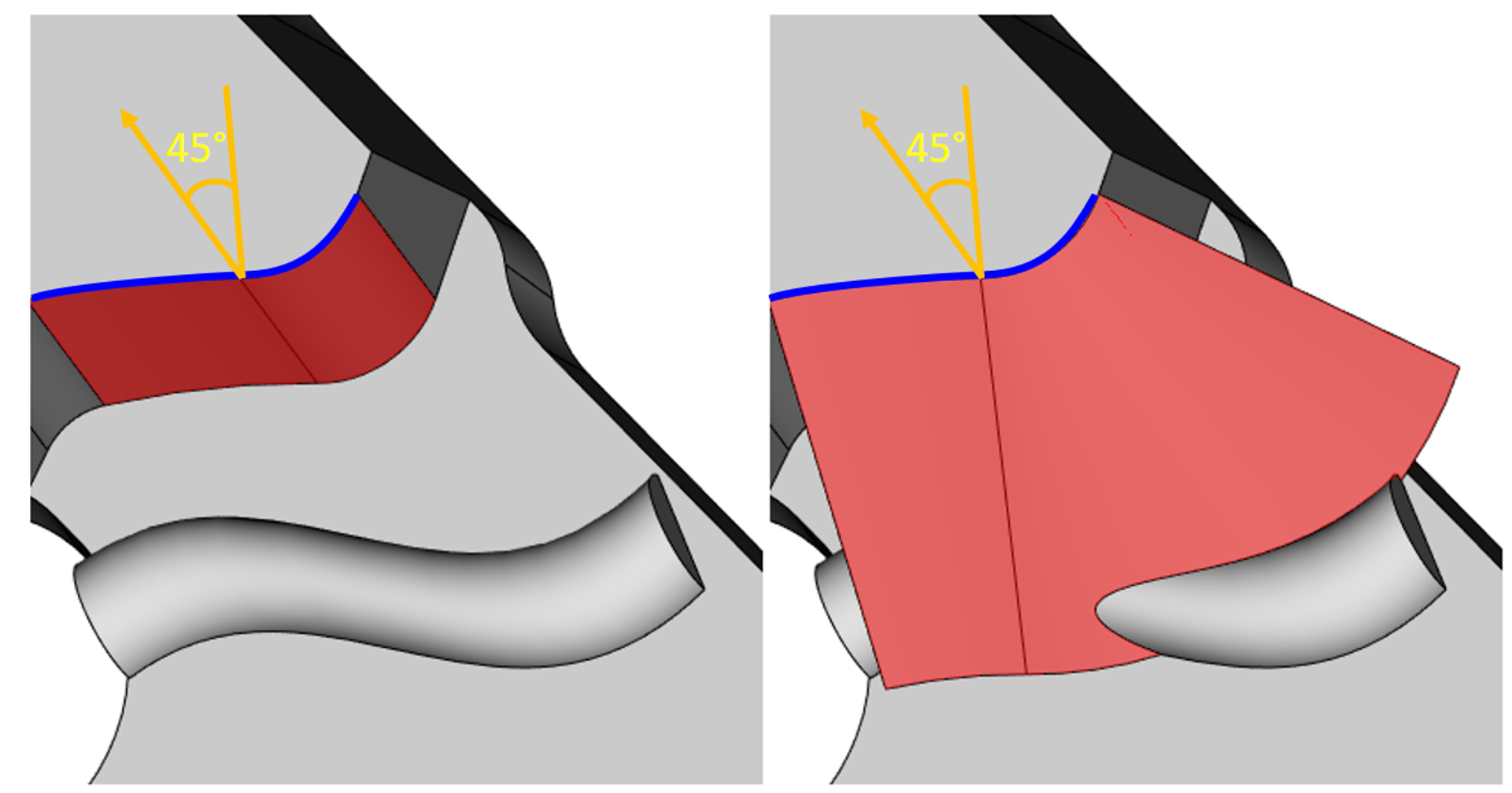
Иллюстрации глобального характера операции «Уклон граней»
В ближайших планах поддержка «поверхностей разъёма», не пересекающих исходное тело, что добавит гибкости в построение ещё более сложной геометрии уклонов. А также реализация целого набора опций по обработке стыковки уклоняемых граней, как между собой, так и с «неподвижными» гранями тела.
Развитие получила функция расширения листового тела. Добавлена возможность затягивания разрывов тела со сложной границей, поддержка расширения сглаженных граней как сглаживаний, расширение до тела.
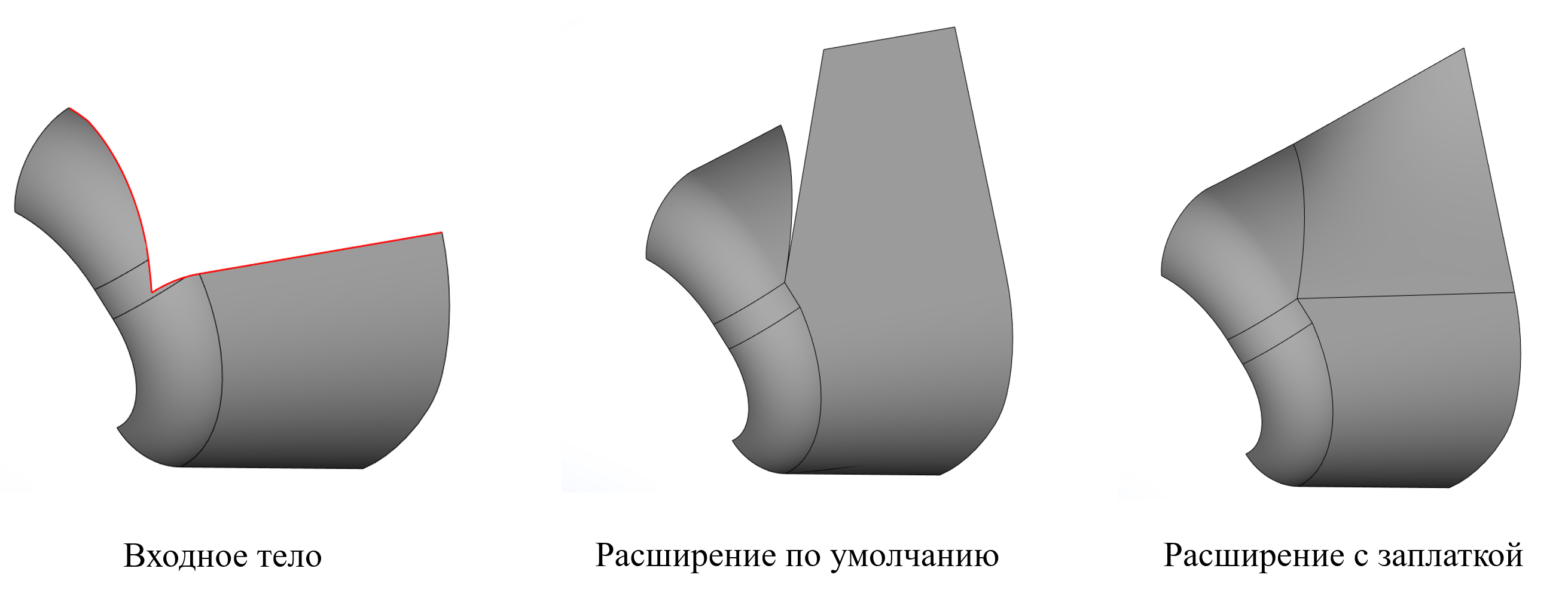
Пример расширения с сохранением неразрывности границы
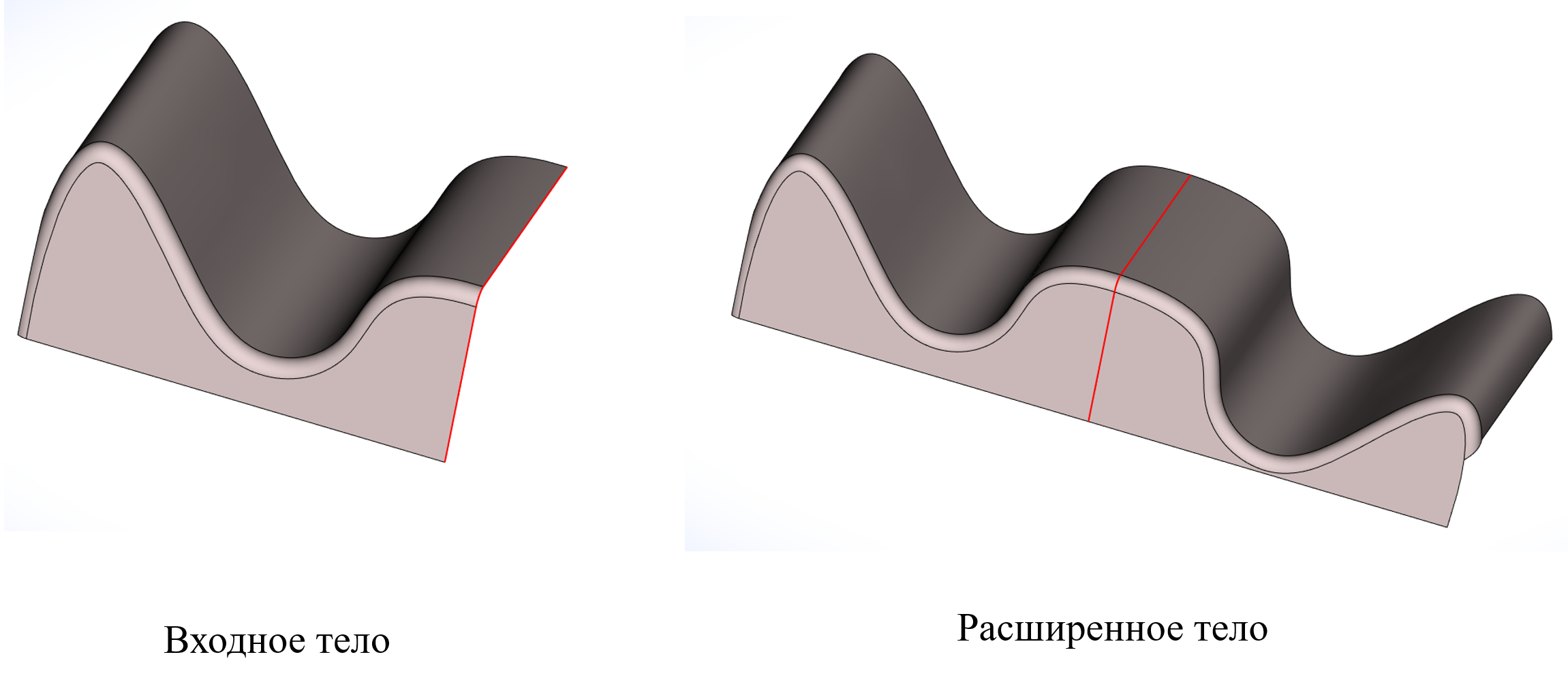
Пример натурального расширения листового тела со сглаживанием
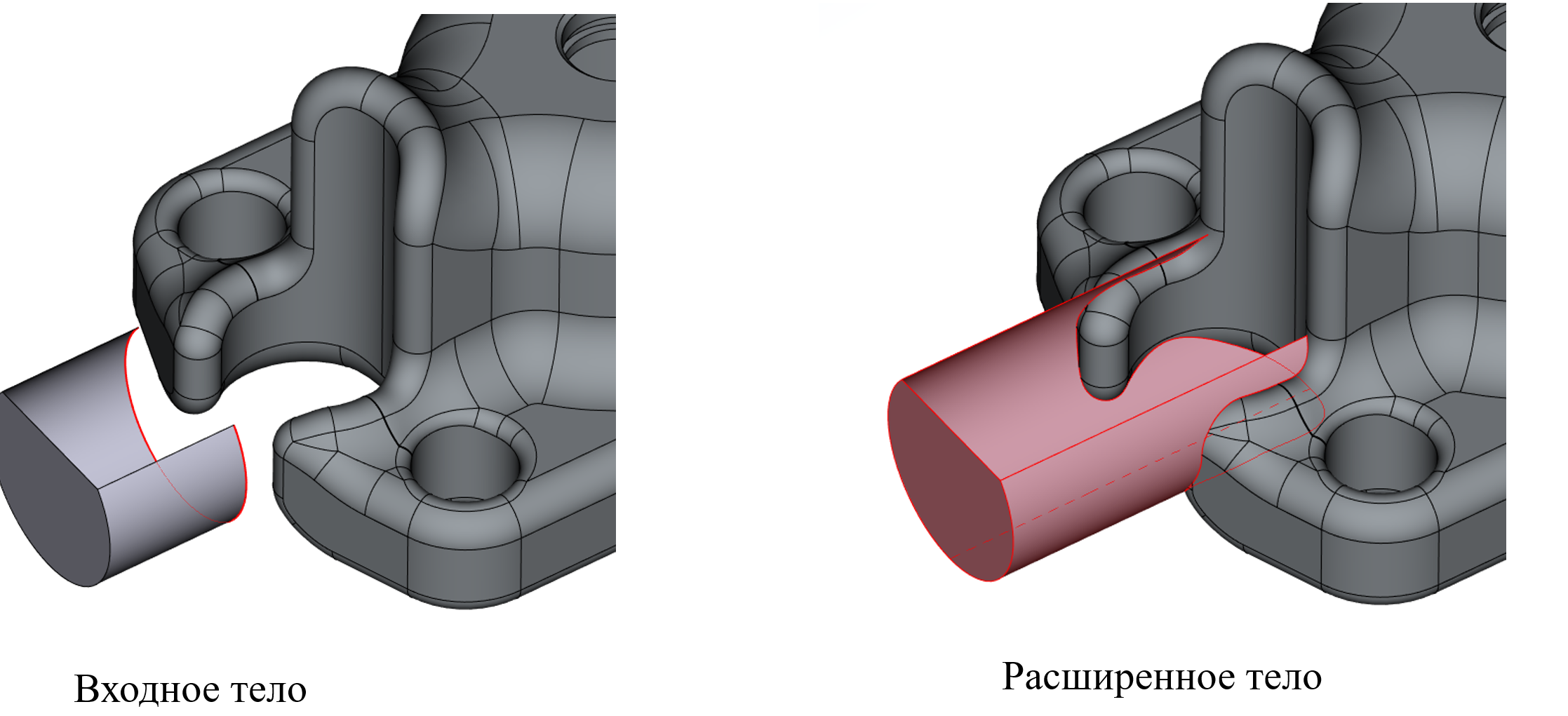
Пример работы опции «расширение до тела»
Традиционно в развитии RGK большое внимание уделяется совершенствованию алгоритмов сглаживания во всех их режимах (сглаживание рёбер, граней и трёхгранном сглаживании). Как отмечалось ещё в прошлом году, важной особенностью архитектуры RGK в этой части является высокая степень унификации топологических алгоритмов. Можно сказать, что алгоритм сглаживания, по сути, один, но он умеет решать разные задачи в зависимости от полученных входных данных. В новой версии было решено изменить API ядра так, чтобы в максимальной степени отразить этот архитектурный момент. В частности, были убраны отдельные классы постоянного и переменного сглаживания, а структура данных изменена таким образом, чтобы позволить прикладному разработчику конечного приложения использовать комбинаторную гибкость алгоритма сглаживания RGK. Конечно, только архитектурными изменениями дело не ограничилось. В новой версии ядра была проделана огромная работа по развитию алгоритма сглаживания во всех аспектах. Как в обработке сложных топологических конфигураций, так и в поддержке новых типов поверхностей сглаживания и совершенствовании математических нюансов их построения. Во-первых, добавлена возможность выбрать ребро, которое необходимо сохранить при формировании переполнения.
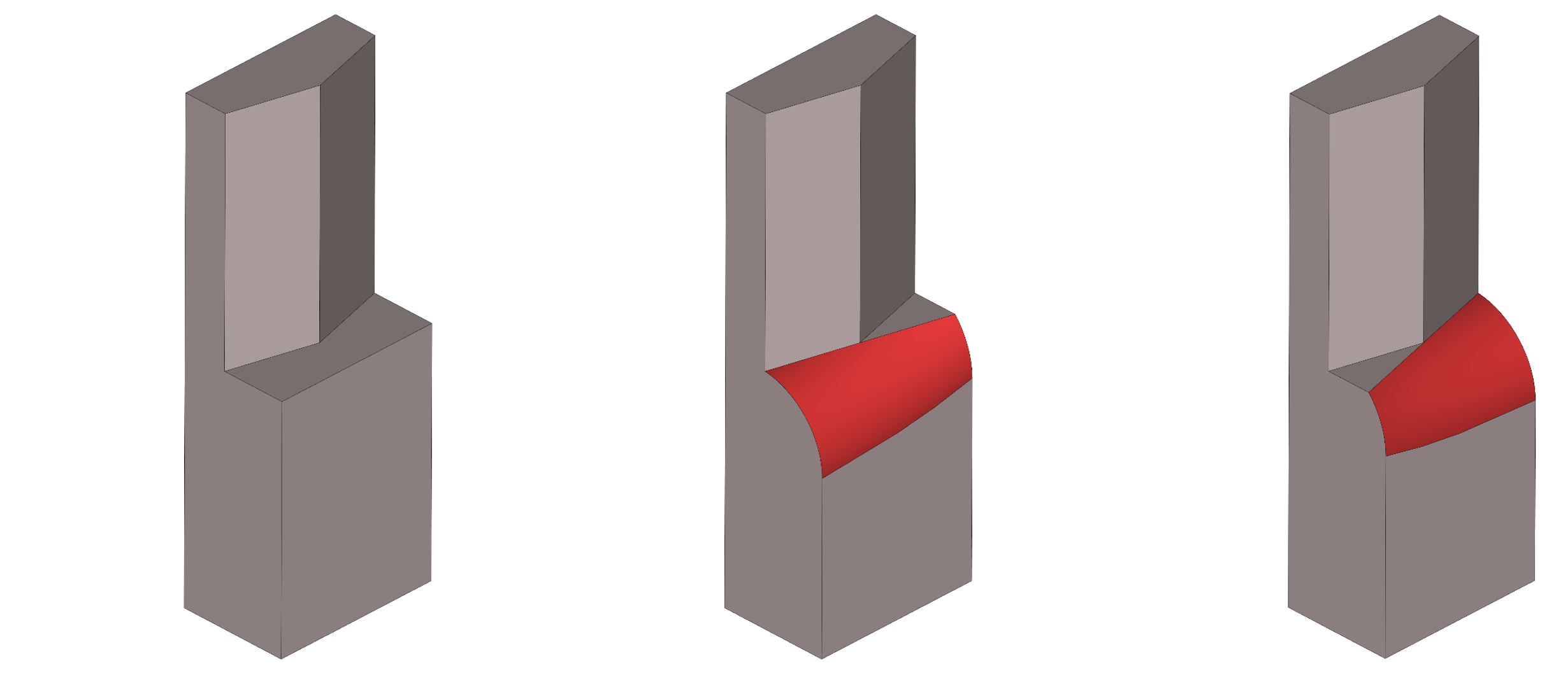
Поведение алгоритма сглаживания при указании разных рёбер для сохранения
Во-вторых, разработан алгоритм принудительной остановки сглаживания на заданной грани или листовом теле.
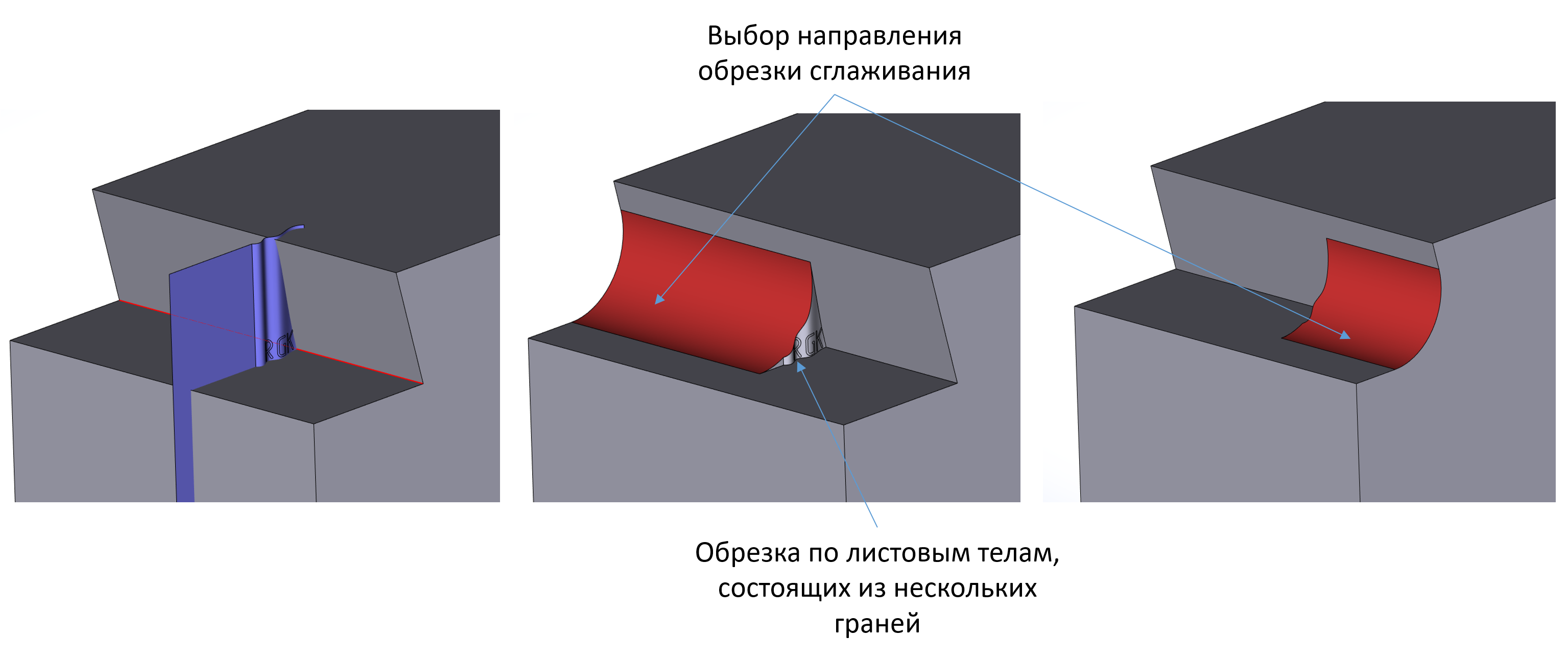
Остановка сглаживания в указанном листовом теле
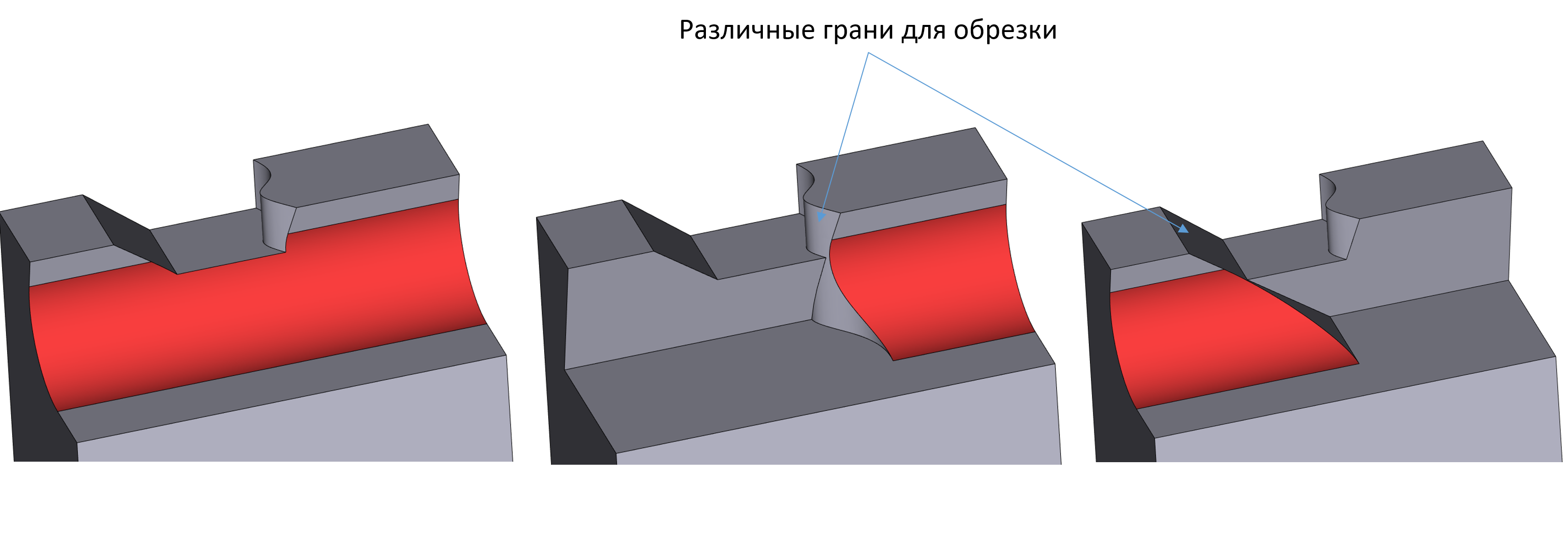
Остановка сглаживания на заданной грани тела
На основе алгоритма останова на указанной геометрии в обработке сложных завершений сглаживаний была добавлена возможность негладкого завершения с формированием корректного твёрдого тела, чтобы дать возможность продолжать моделирование другими инструментами.
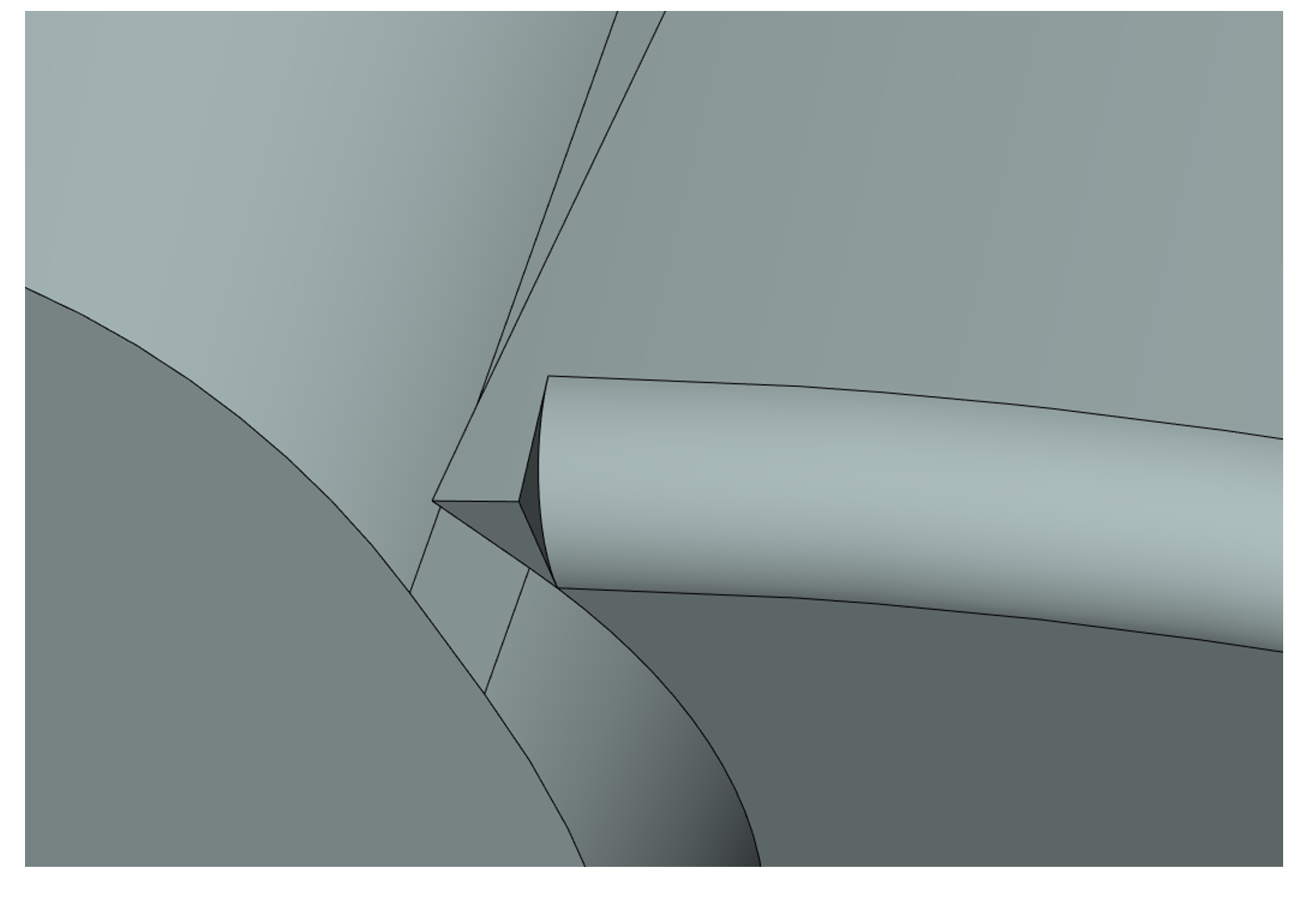
Остановка сглаживания при невозможности гладкого завершения
Дальнейшее развитие получили алгоритмы встраивания сглаживающего листа. Добавлена опция необходимости учёта топологии тела в зоне листа сглаживания.
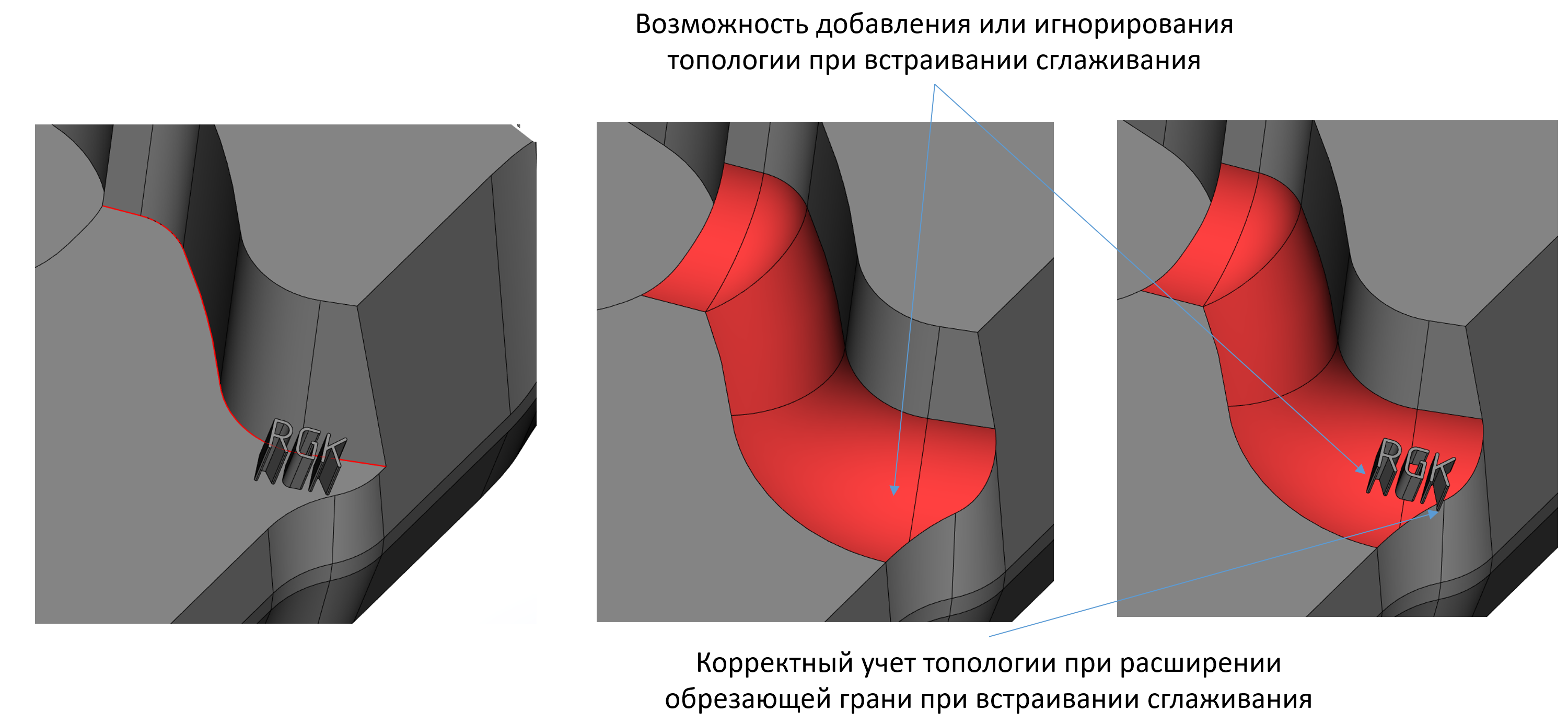
Иллюстрация включения или отключения опции учёта топологии в зоне сглаживания
Значительно расширены возможности алгоритма сглаживания при обработке сложных топологических конфигураций на модели как для постоянного, так и для переменного сглаживания.
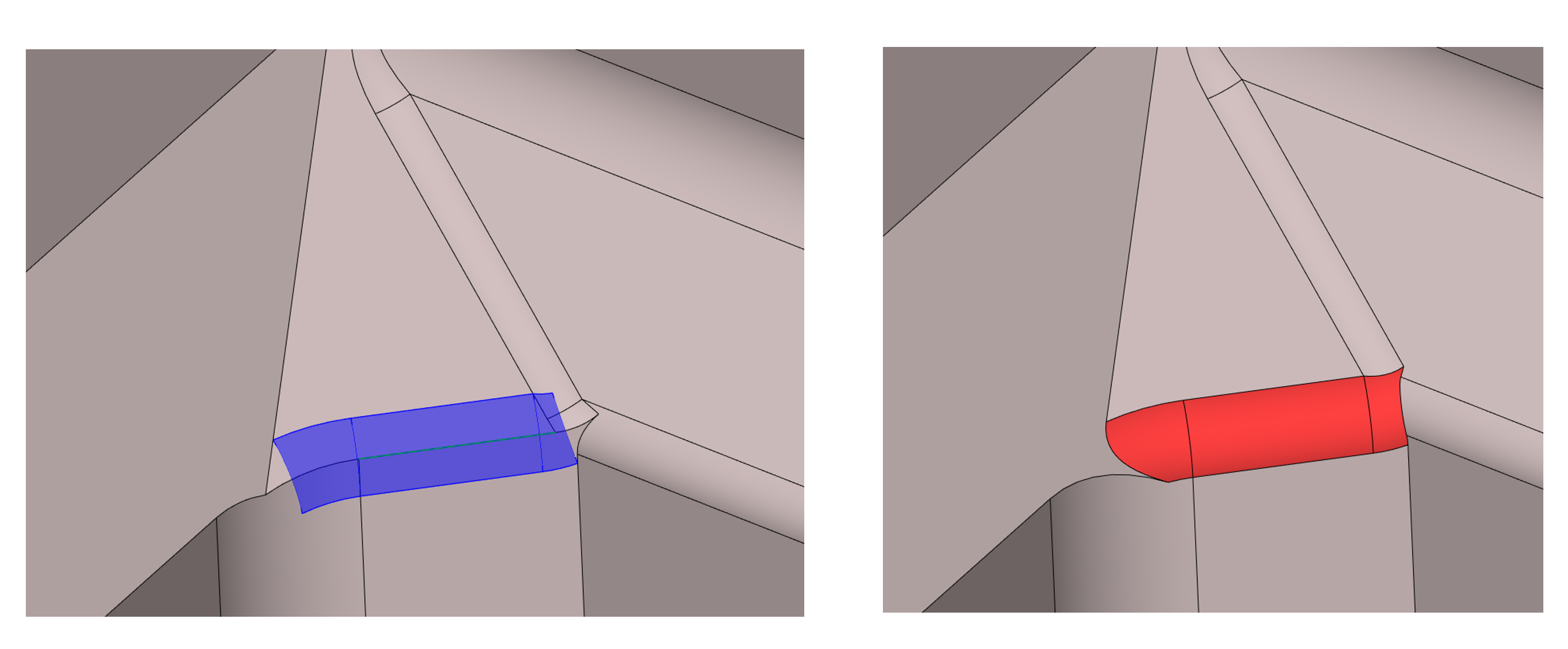
Пример встраивания рёберного сглаживания в сложных топологических конфигурациях
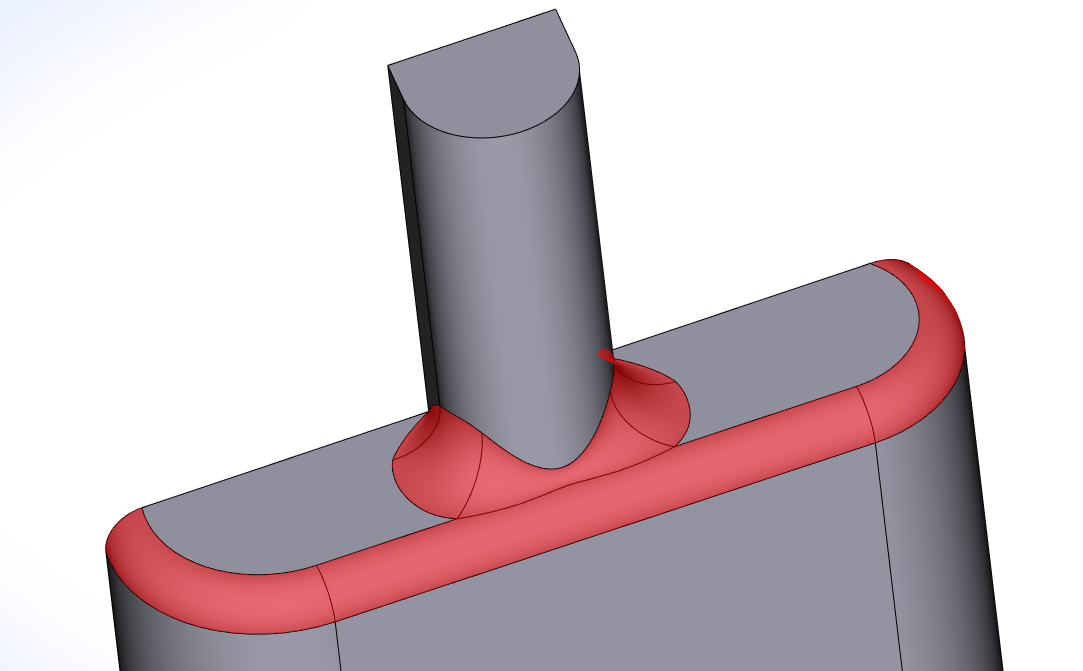
Пример встраивания трёхгранного сглаживания

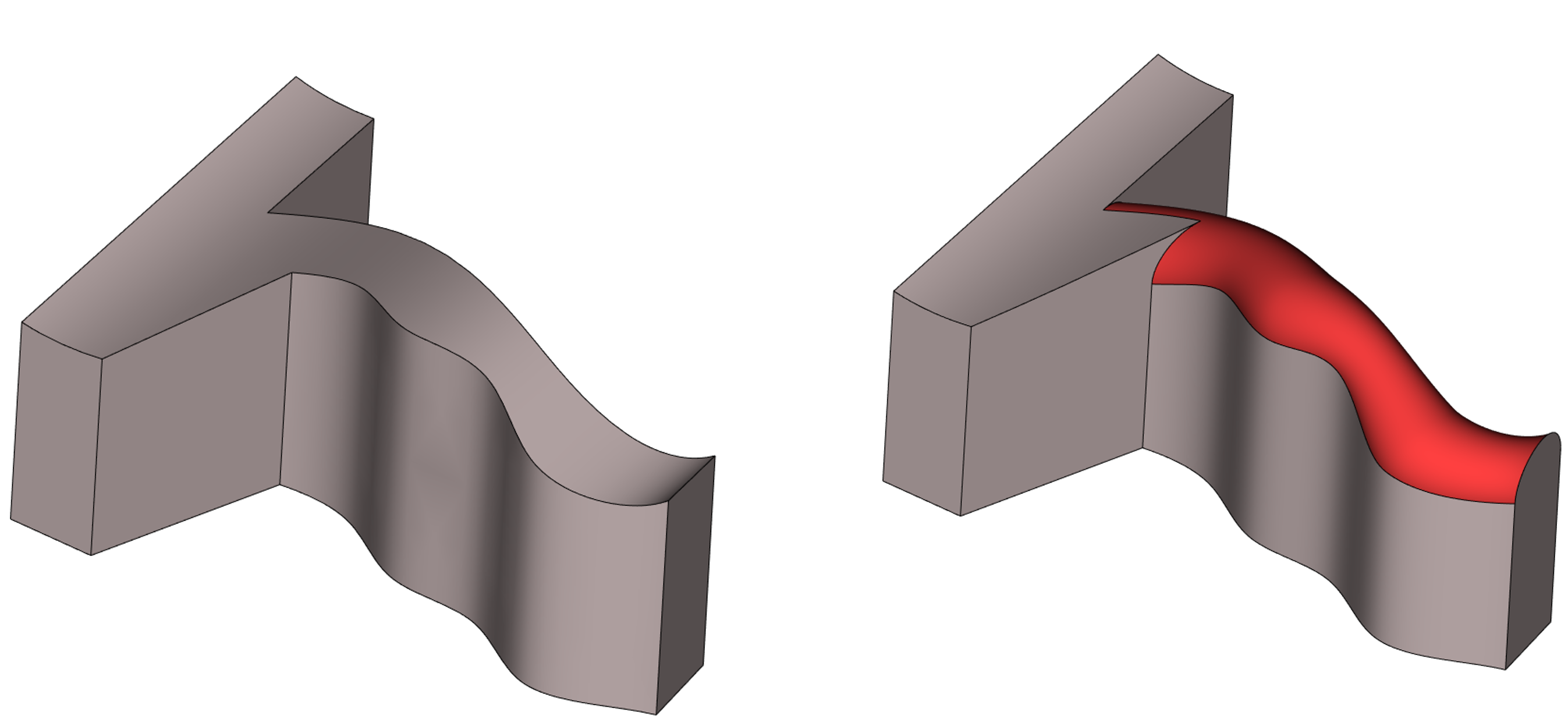
Расширение возможностей обработки участков с кривизной малого радиуса – теперь топология в зоне формирования прокатывания малого радиуса может быть произвольной
Пример перекрытия сглаживаний переменного радиуса

Пример взаимного перекрытия сглаживаний с симметричной обрезкой сглаживающих листов
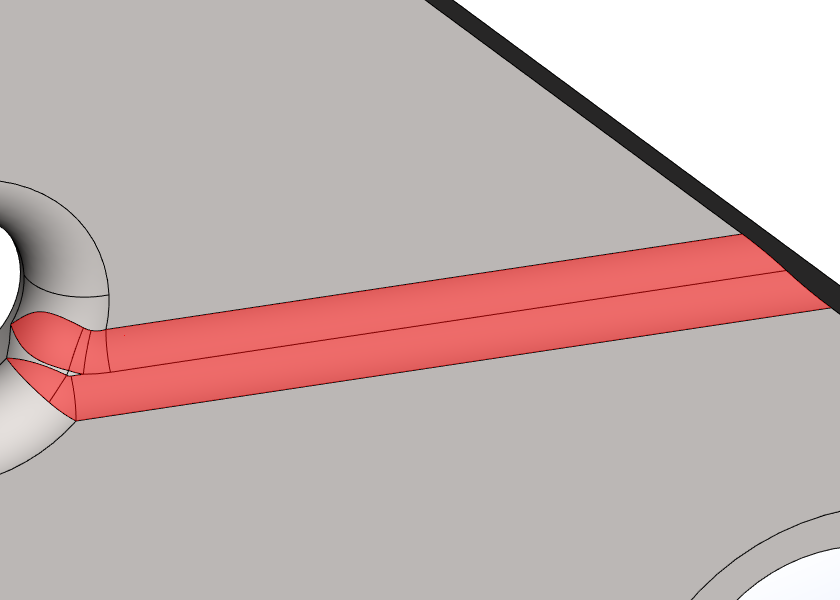
Пример перекрытия сглаживаний на нескольких гранях
Введено управление порядком прокатывания сглаживающего «шарика», что позволяет варьировать форму поверхности в вершинах, где сходятся рёбра разной выпуклости.
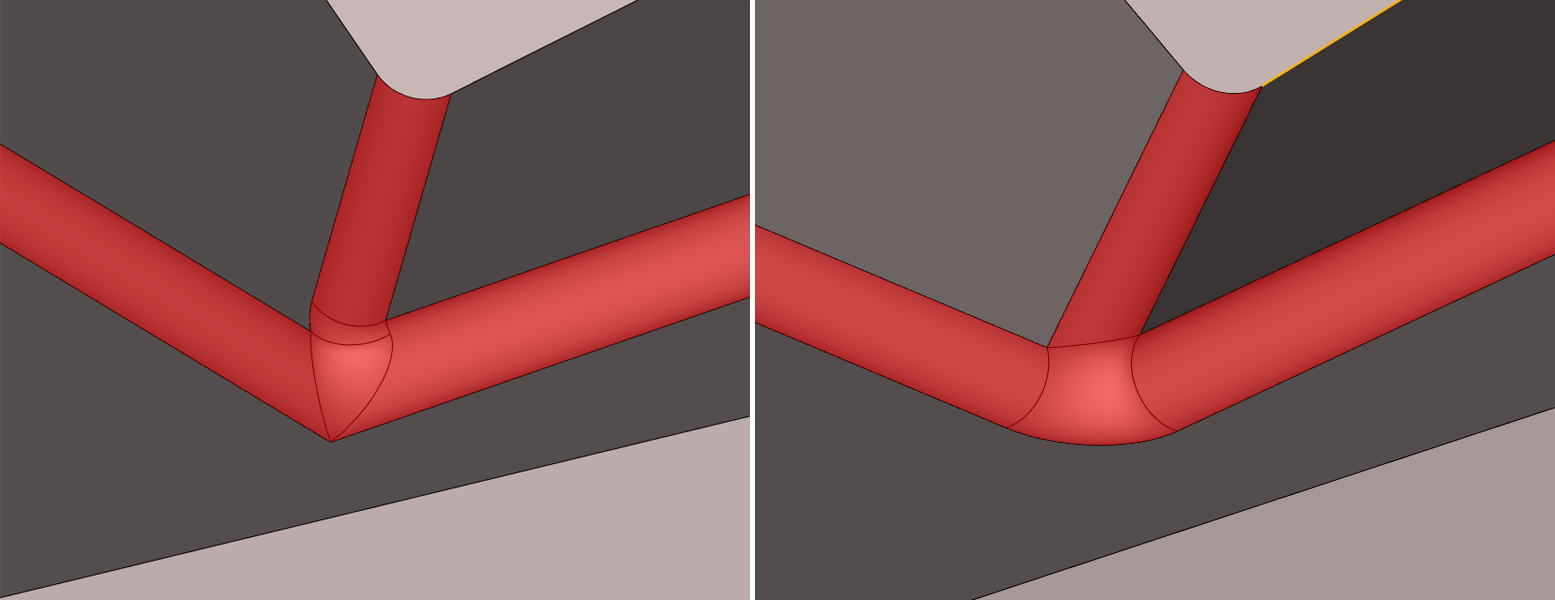
Пример формирования поверхности сглаживания при разной последовательности прокатывания шарика
Теперь поддерживается возможность обработки угла модели с прокатыванием шарика, а не только с обрезкой сглаживающих поверхностей.
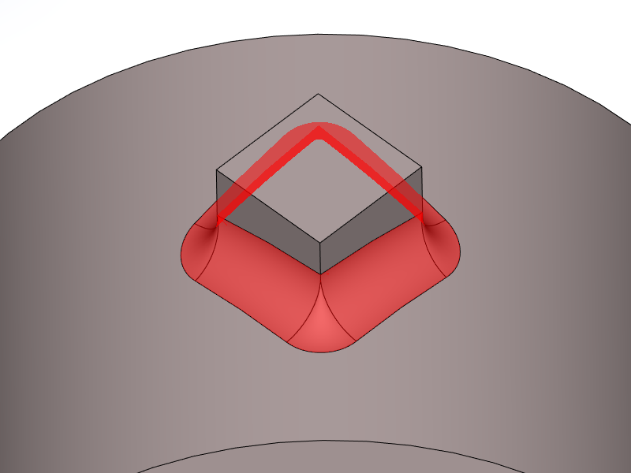
Иллюстрация «гладкого» угла сглаживания при сохранении острого ребра на теле
В связи с тем, что как для сглаживания рёбер, так и для сглаживания граней используется один алгоритм, то и обработки различных случаев стыковки граней выполняются аналогичным образом.
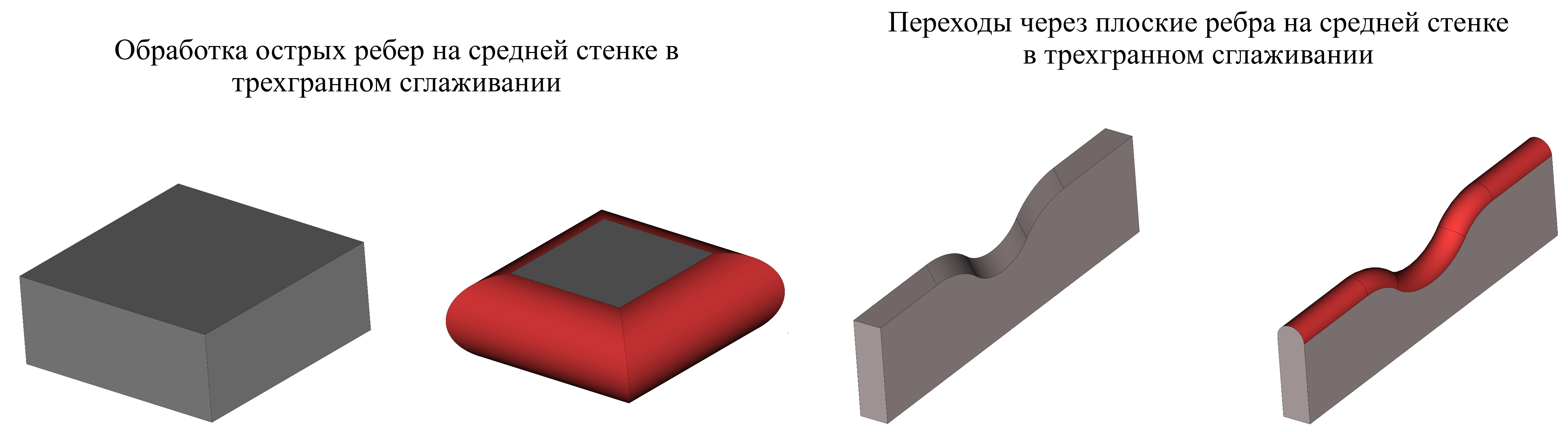
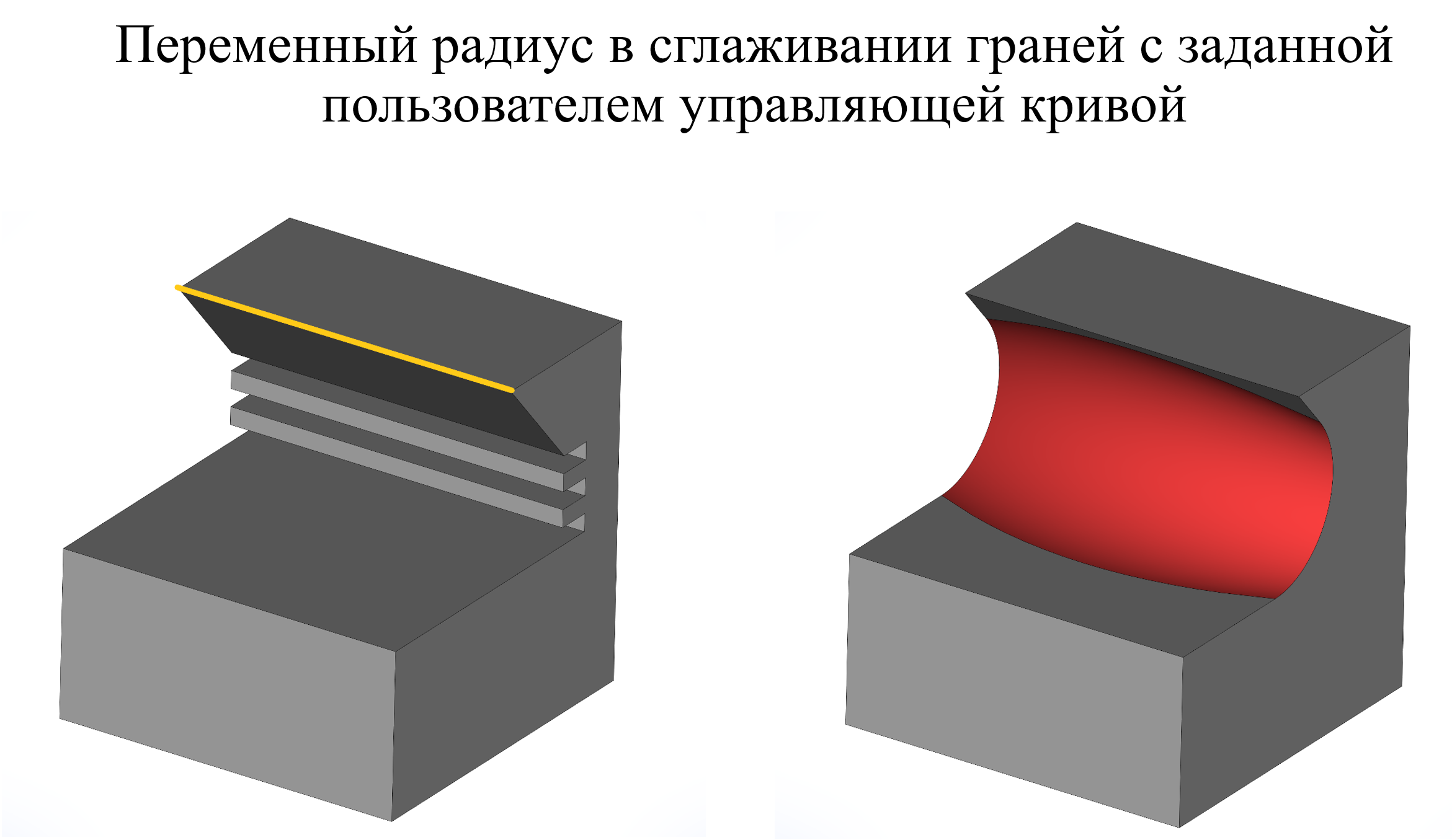
Примеры поведения алгоритма сглаживания в граневом и трёхгранном режимах
Функциональность сглаживания RGK, как известно, работает не только на твёрдых телах, но и на листовых. Причём с точки зрения API нет никакого отличия в операциях с разными типами топологических моделей.
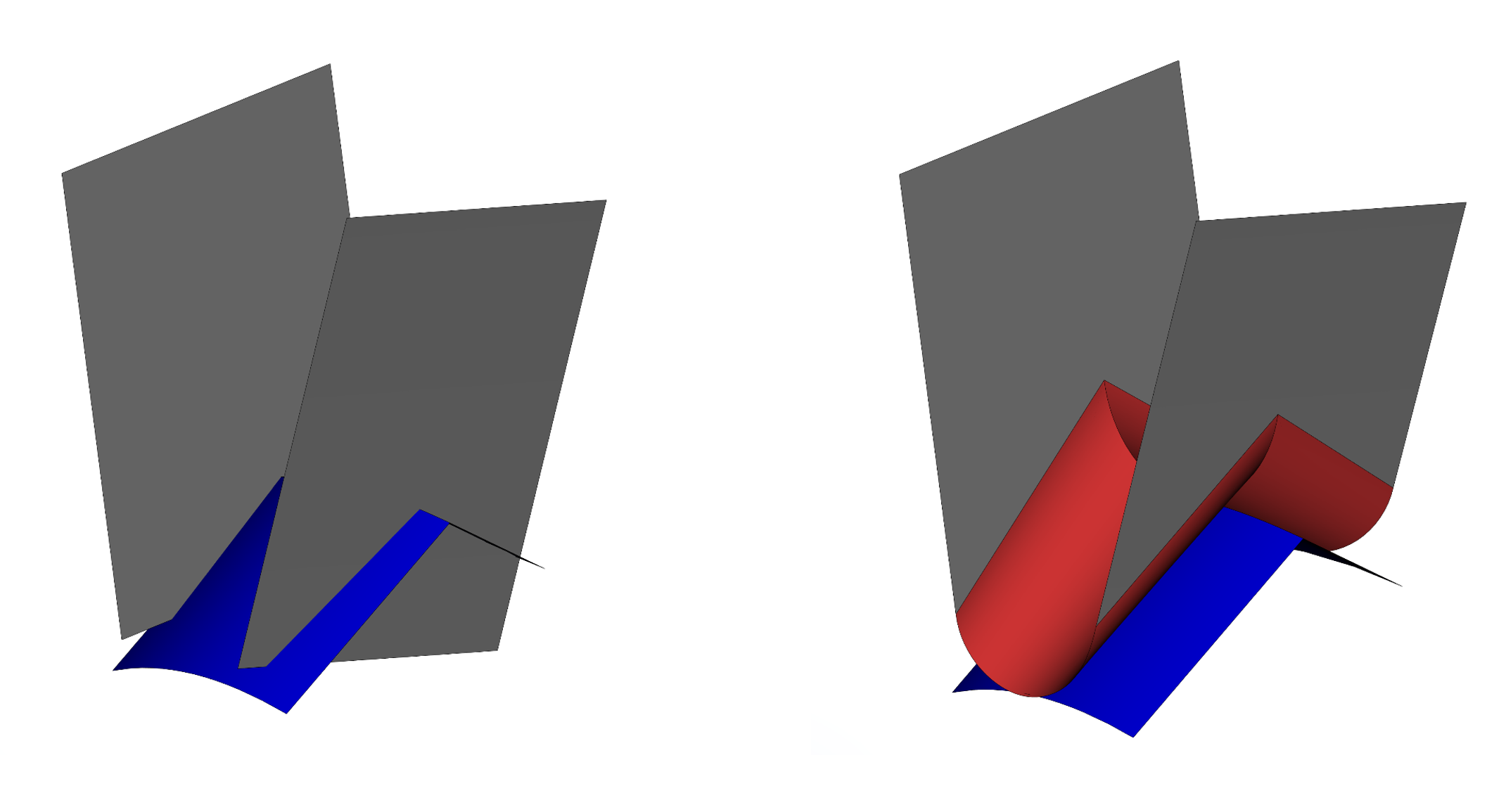
Пример работы трёхгранного сглаживания на наборе листовых тел
Помимо улучшений и развития топологических алгоритмов сглаживания, существенное развитие получила и его геометрическая часть. В частности, много усилий было приложено к разработке алгоритмов борьбы с самопересечениями поверхностей сглаживания. Такая ситуация нередко возникает в практических задачах, и промышленное ядро должно обладать развитыми инструментами коррекции геометрии с гарантией отсутствия самопересечений. Задача это весьма сложная и не может быть решена одним алгоритмом – требуется разработать набор инструментов и выработать правила их практического применения в алгоритмах ядра. Именно такая работа сейчас и ведётся разработчиками RGK, и в новой версии можно увидеть первые результаты этой работы. Вот, собственно, о какой проблеме идёт речь:
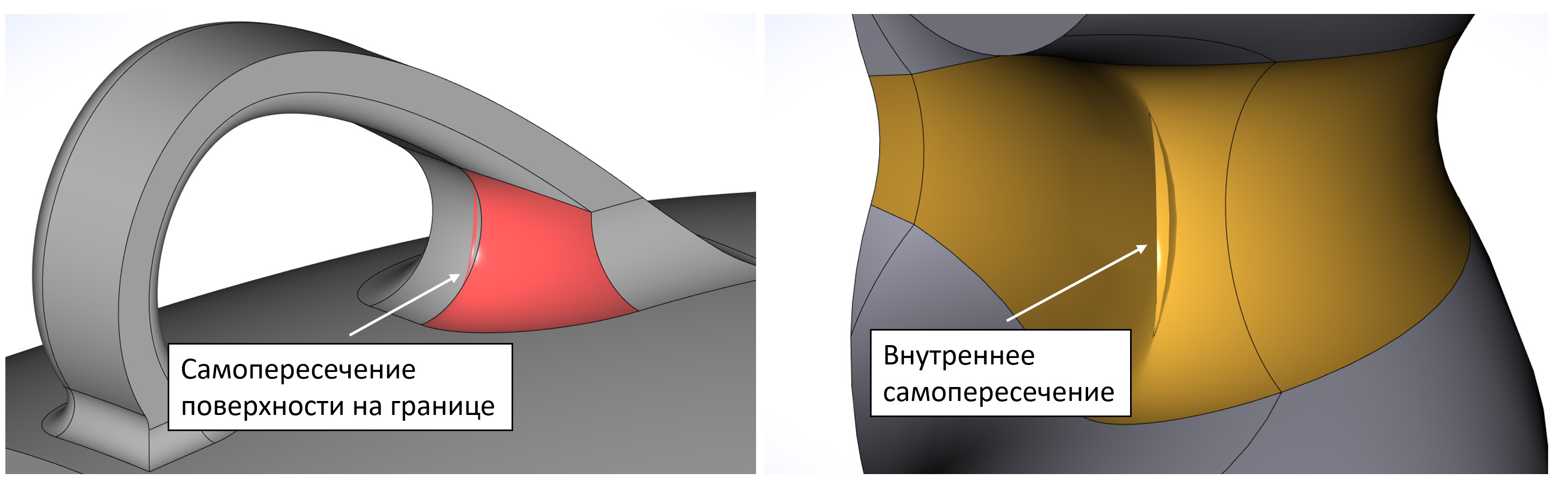
Примеры самопересечений поверхности сглаживания
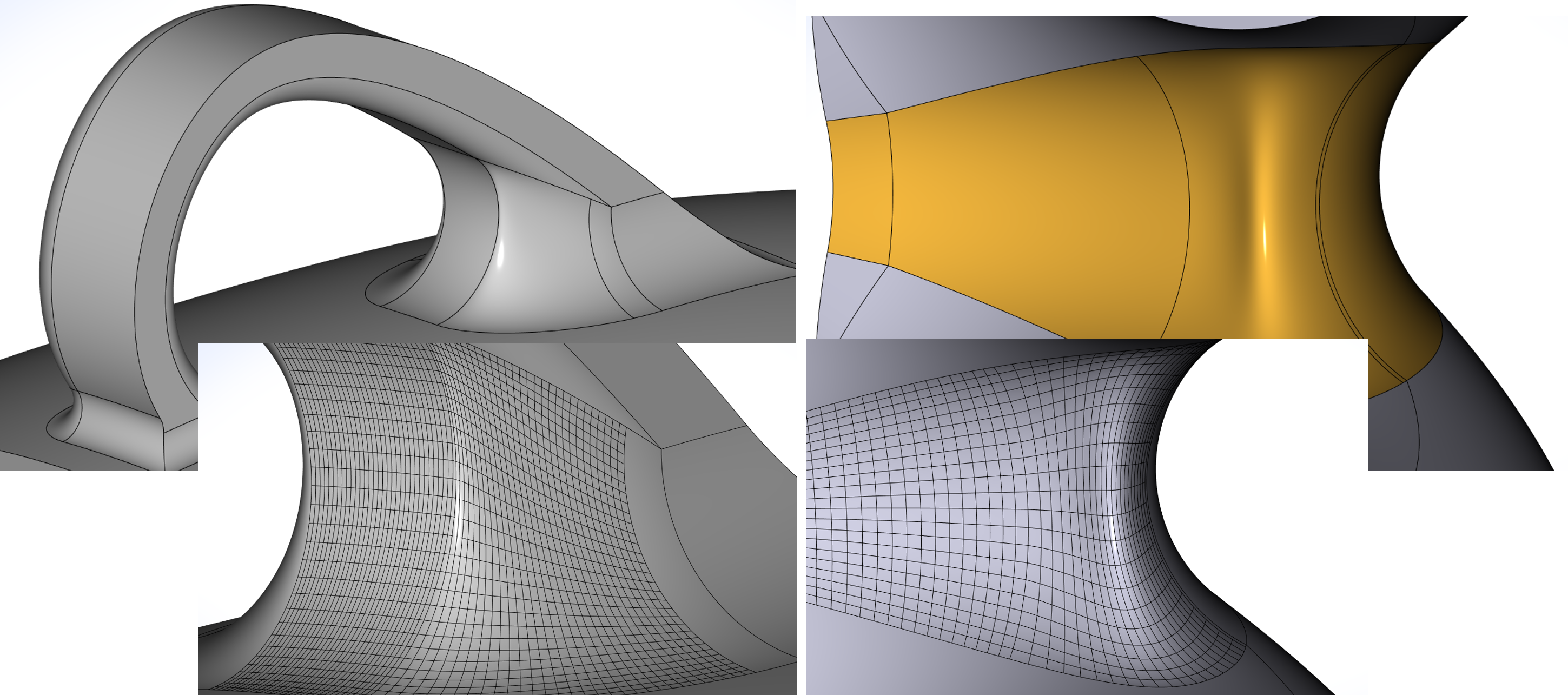
Пример работы одного из алгоритмов исправления самопересечений поверхностей сглаживания
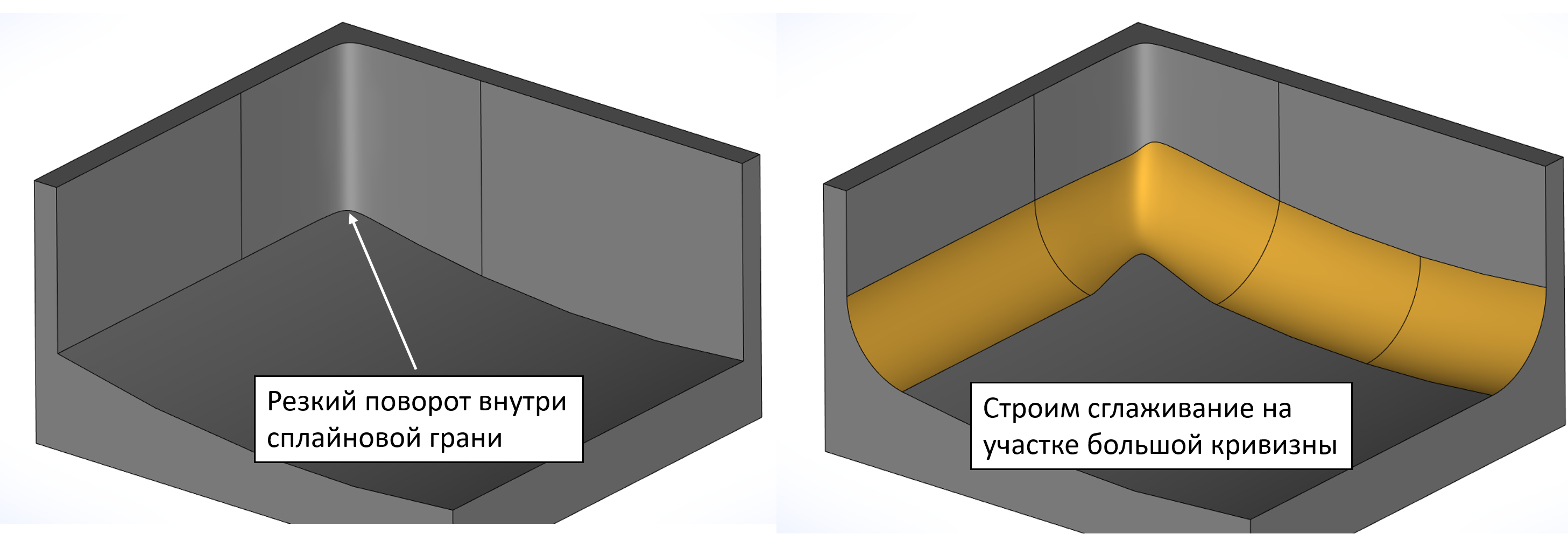
Пример работы алгоритма коррекции самопересечения в зонах высокой кривизны сглаживаемых поверхностей
Усовершенствованиям подверглись алгоритмы построения дискового сглаживания, а также добавился новый тип сглаживающих поверхностей – поверхности «изопараметрического» сглаживания. В дисковом сглаживании теперь поддерживается произвольный закон радиуса и форма сечения.
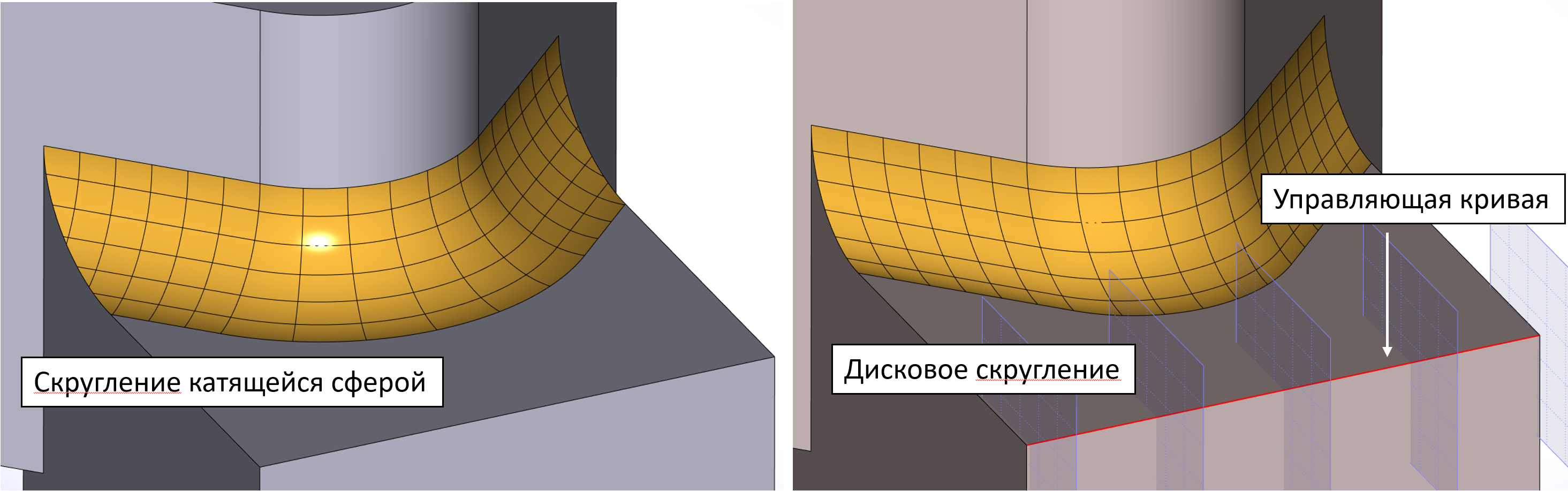
Иллюстрация отличия «традиционного» сглаживания с прокатыванием шарика от дискового
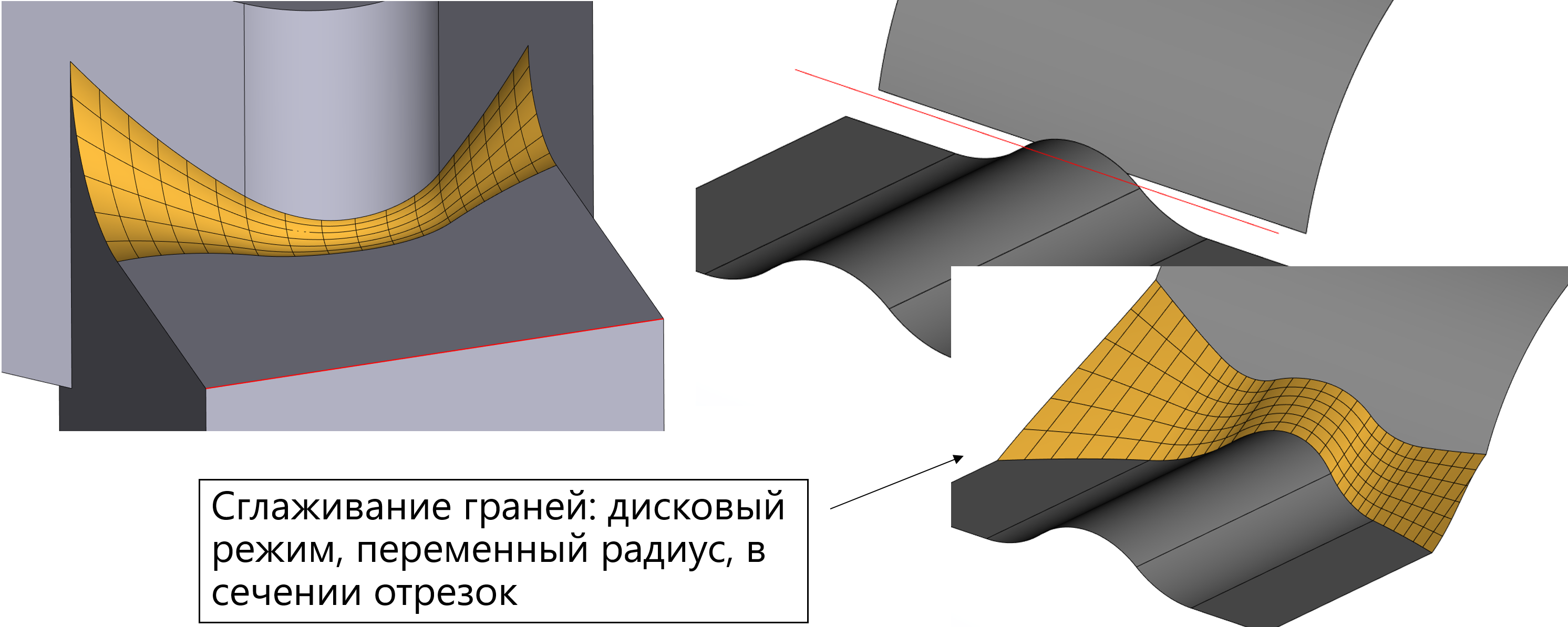
Пример работы режима дискового сглаживания на твёрдом и листовых телах
Естественным образом дисковое сглаживание доступно и в сопряжении трёх граней.
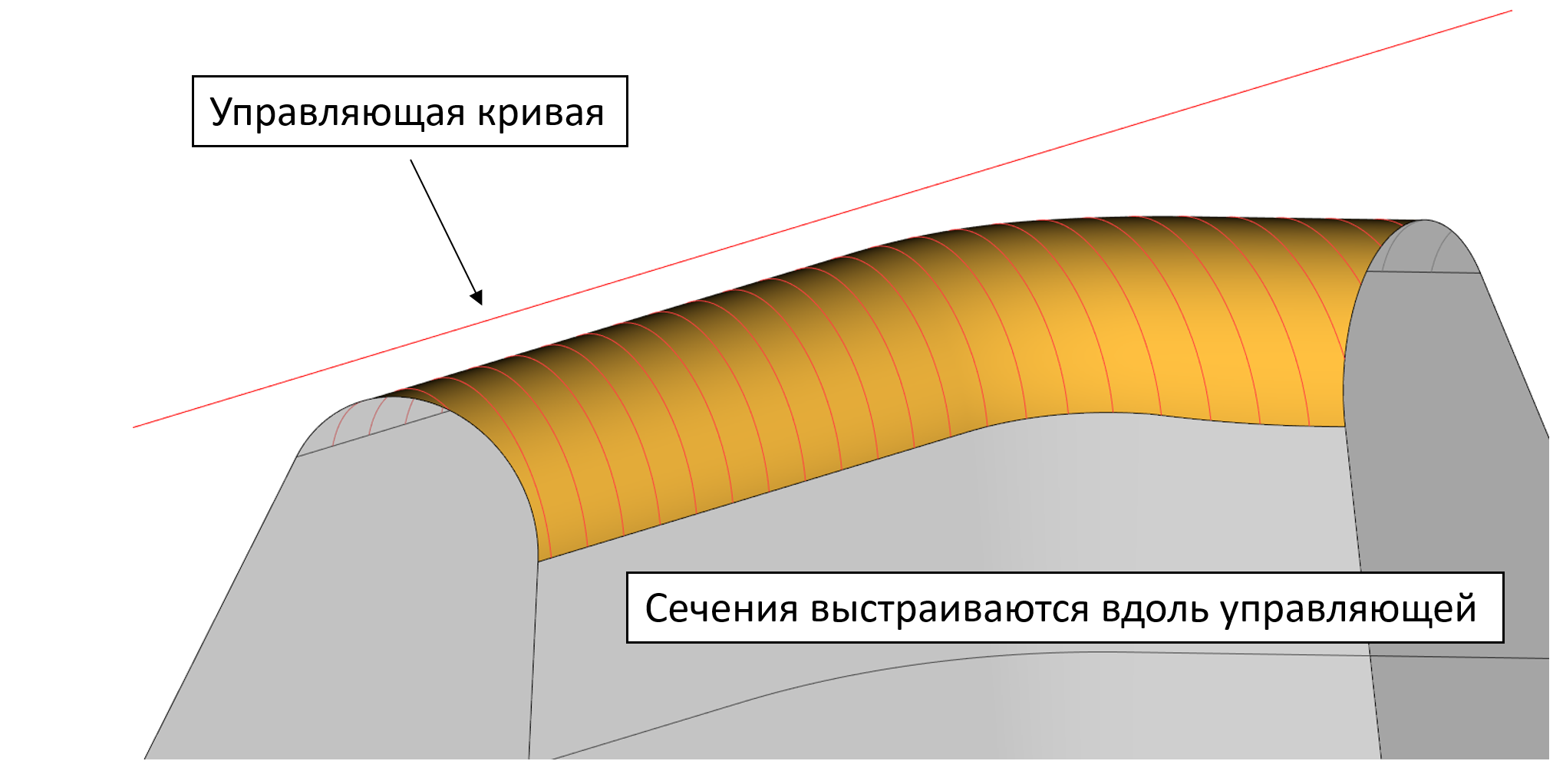
Пример применения режима дискового сглаживания в трёхгранном режиме
Помимо «традиционных» режимов сглаживания, как отмечалось выше, был разработан алгоритм для построения «изопараметрического» сглаживания. Суть его в том, что плоскость сечения сглаживающей поверхности привязана к изопараметрическим линиям одной из родительских граней.
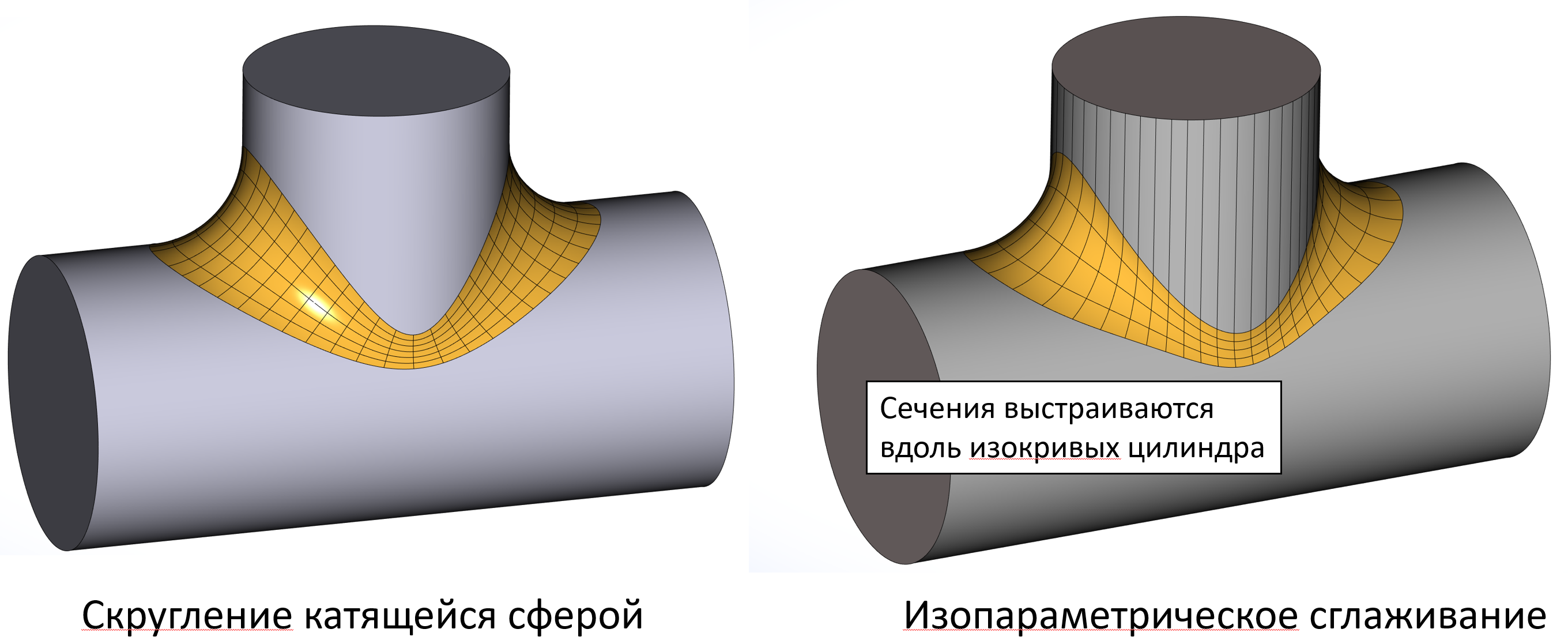
Иллюстрация отличия изопараметрического сглаживания от поверхности катящегося шарика
Как нетрудно предположить, изопараметрическое сглаживание, как и два других типа, допускают управление радиусом и формой сечения.
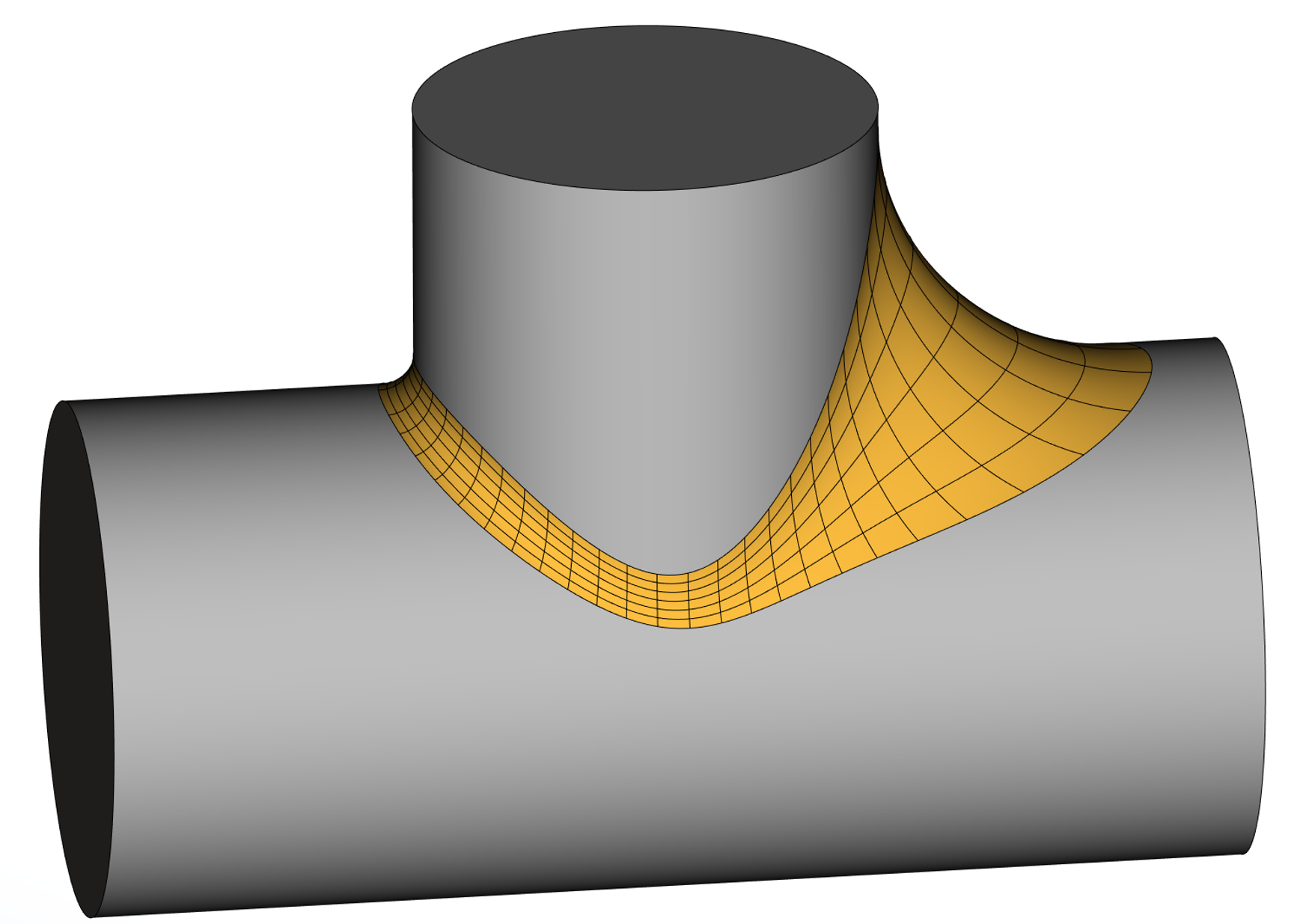
Пример изопараметрического сглаживания с переменным сечением
Отдельной большой работой в направлении повышения гибкости алгоритмов сглаживания в новой версии RGK была разработка новых типов поверхностей сглаживания с сохранением геометрии кривой. Напомним, что в предыдущих версиях ядра была возможность построения поверхности с сохранением ребра модели так, чтобы обеспечивалось касание с противоположной гранью, в то время как касания с гранью, содержащей сохраняемое ребро, не требовалось. Это так называемое «переполнение» сглаживания. Теперь же в ядро добавлена возможность сохранение такого касания двумя способами. Так называемые «симметричный» и «конический» режимы. В первом из них ответная опорная кривая сглаживания как бы повторяет форму сохраняемого ребра, во втором следует заданному закону радиуса.
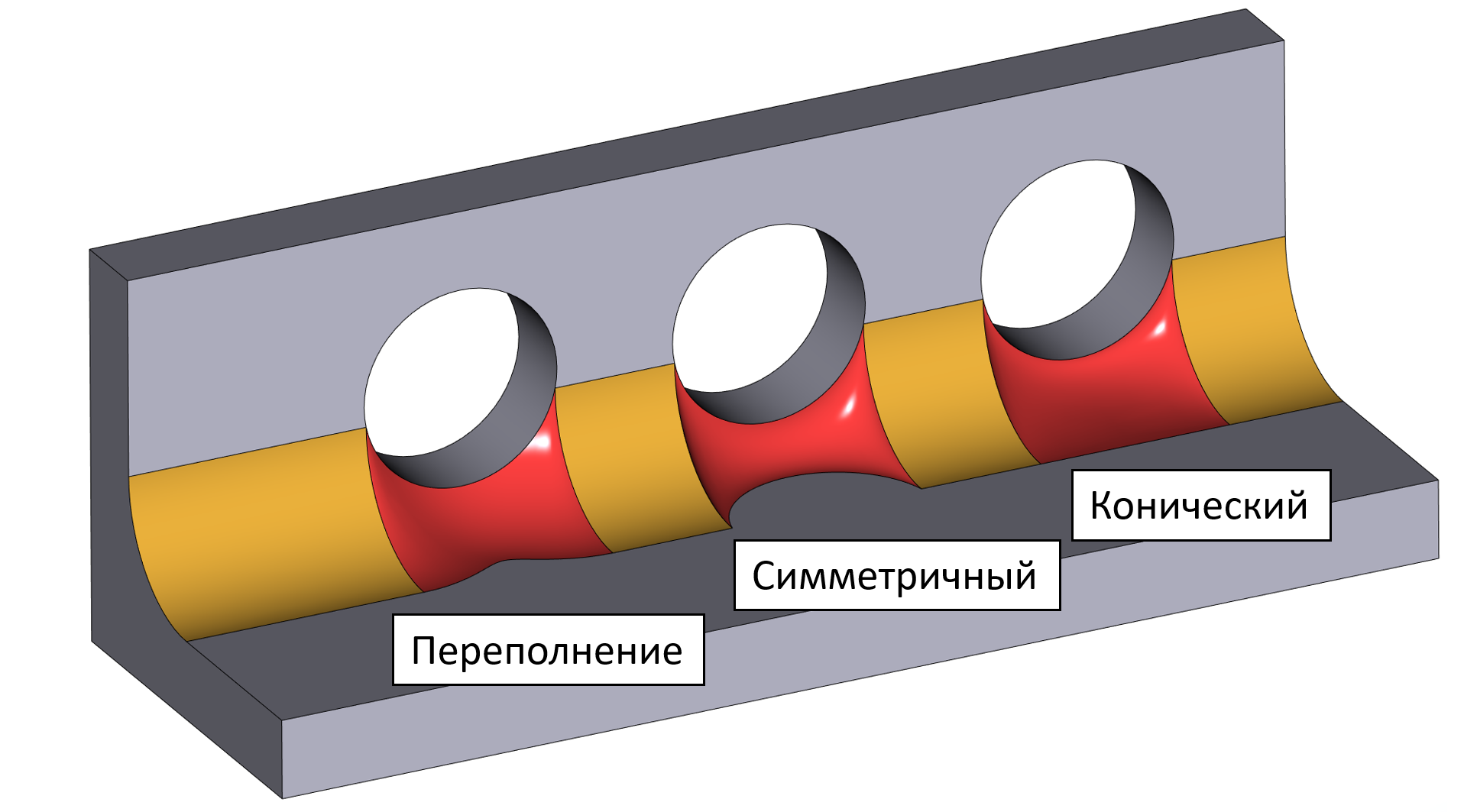
Иллюстрация режимов сглаживания с сохранением ребра
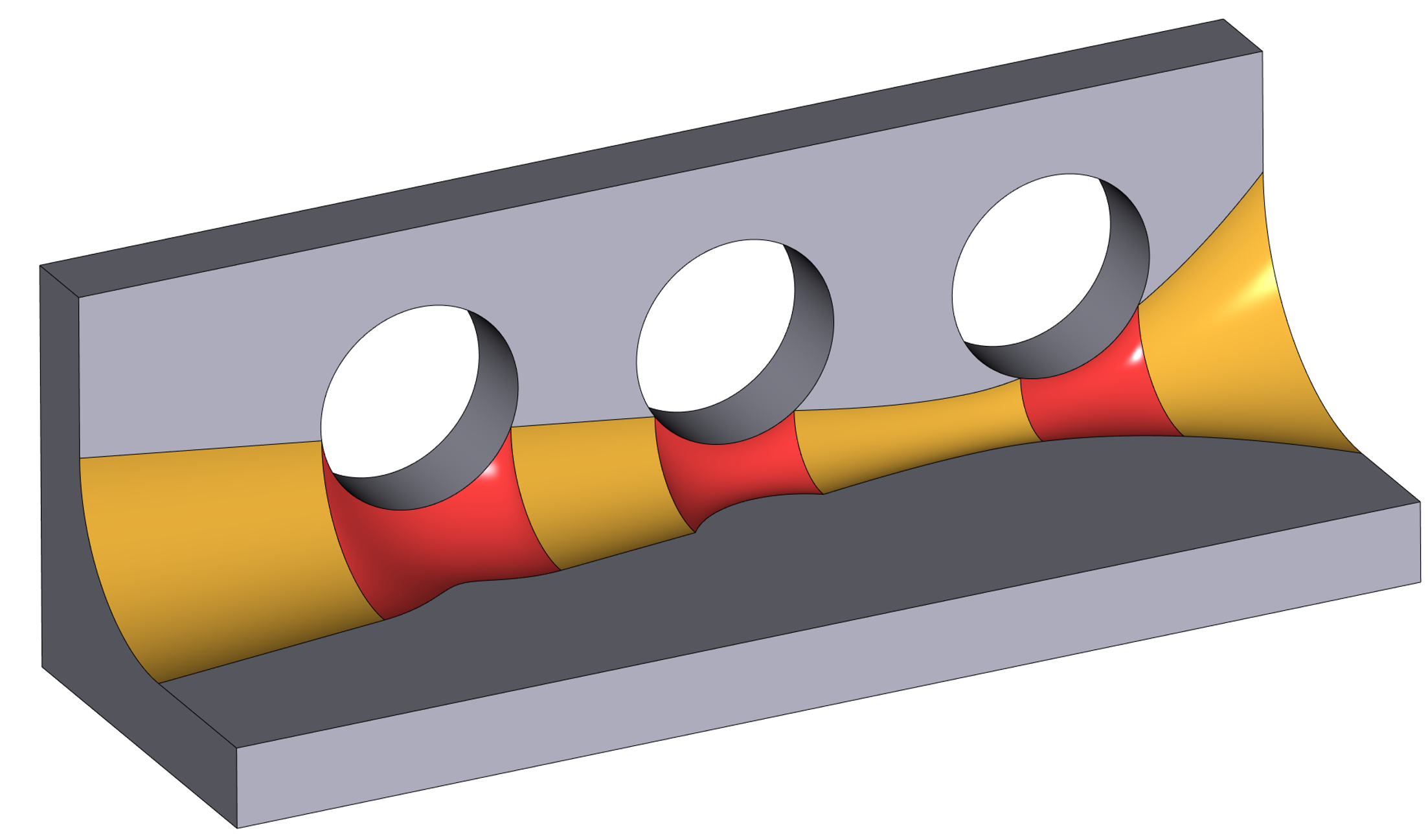
Иллюстрация работы режимов сохранения ребра в том числе и с переменным радиусом
Развитие этой функциональности активно продолжается. В ближайшее время планируется добавить, в частности, поверхности с двумя заданными опорными кривыми в комбинации с законом радиуса. Кроме того, разрабатывается математика улучшения качества стыковки поверхностей переменного радиуса в различных сложных случаях. Текущие результаты этих исследований обнадёживают, и мы рассчитываем, что в ближайших обновлениях ядра сможем более подробно их продемонстрировать в виде готовой функциональности.
Не осталась в стороне от усовершенствований и функциональность построения фасок. Добавлены два новых способа задания размеров фаски: двумя смещениями от вершины – пересечения касательных к родительским граням и смещением и прилежащим углом.
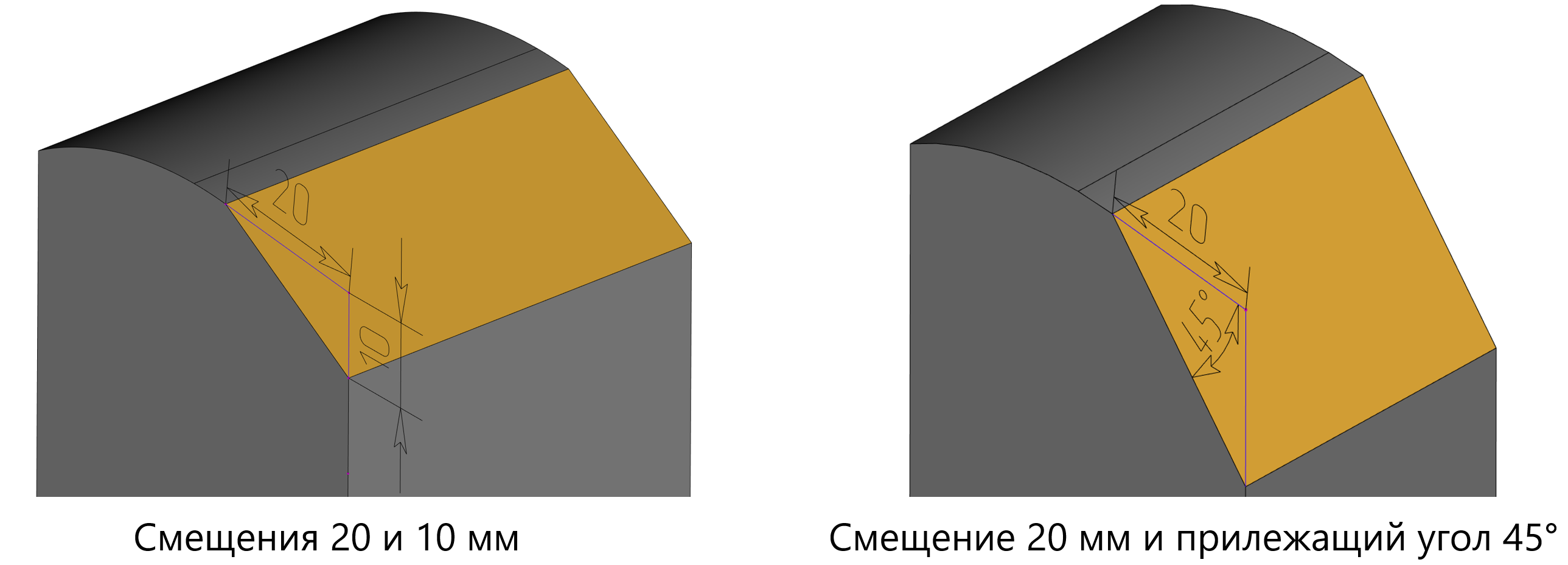
Иллюстрация новых способов задания размера фаски на ребре
Если говорить об интересных текущих задачах, которые решаются коллективом разработчиков RGK в настоящий момент, следует отметить работы по новому алгоритму построения поверхности затягивания области произвольной конфигурации. С одной стороны, это будет мощный инструмент для внутреннего использования в различных алгоритмах ядра, а с другой — он будет доступен и прикладным разработчикам, использующим ядро через соответствующий API. Пока рано раскрывать технические подробности. Приведём лишь несколько визуальных примеров работы нового инструмента.

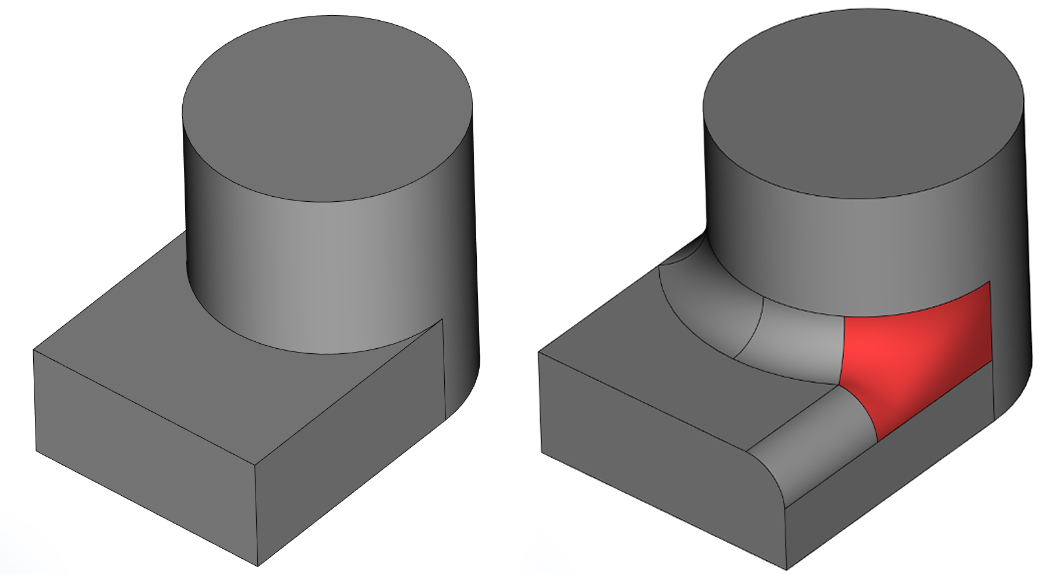
Новая поверхность затягивания в задаче гладкого заполнения вершинной области в сглаживании

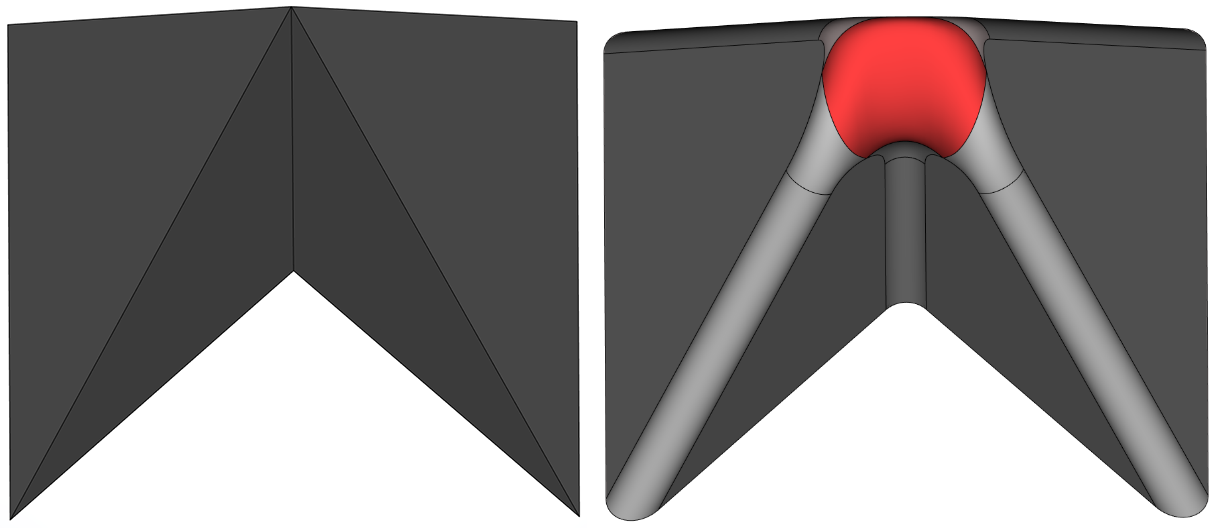
Новая поверхность затягивания в задаче гладкого заполнения области Y-формы в сглаживании
Изменения в API и общей функциональности
Помимо развития функций моделирования за минувший год была проделана большая работа по совершенствованию внутренних алгоритмов ядра, что и позволило наращивать функциональность такими высокими темпами. Усовершенствованию подверглись все основные компоненты, как внутренние, так и доступные извне: алгоритмы построения линий пересечения и проецирования, булевы операции, фасетер, алгоритмы проецирования с удалёнными невидимыми линиями, верификатор топологической модели (чекер) и многие другие. С одной стороны, проведённая работа позволила ещё больше унифицировать внутренние инструменты ядра, что упрощает его дальнейшее развитие, с другой позволяет улучшать качество и скорость программного кода. В качестве примера эффекта от такой работы хочется привести несколько иллюстраций, показывающих текущий статус и изменения в скорости работы функции генерации полигональной модели. Все приведённые ниже примеры касаются построения сеток с одинаковыми параметрами по точности на одном и том же компьютере в многопоточном режиме.
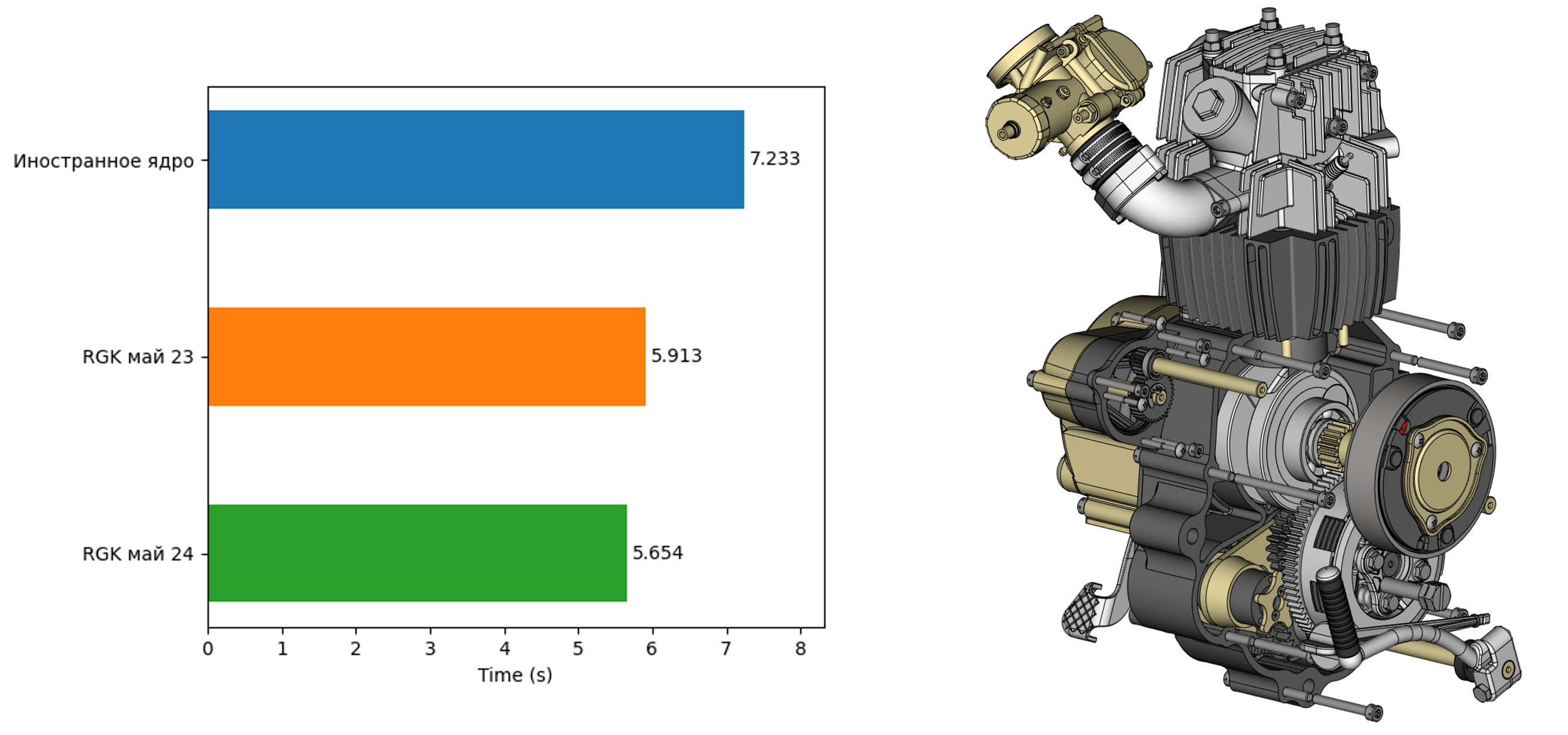
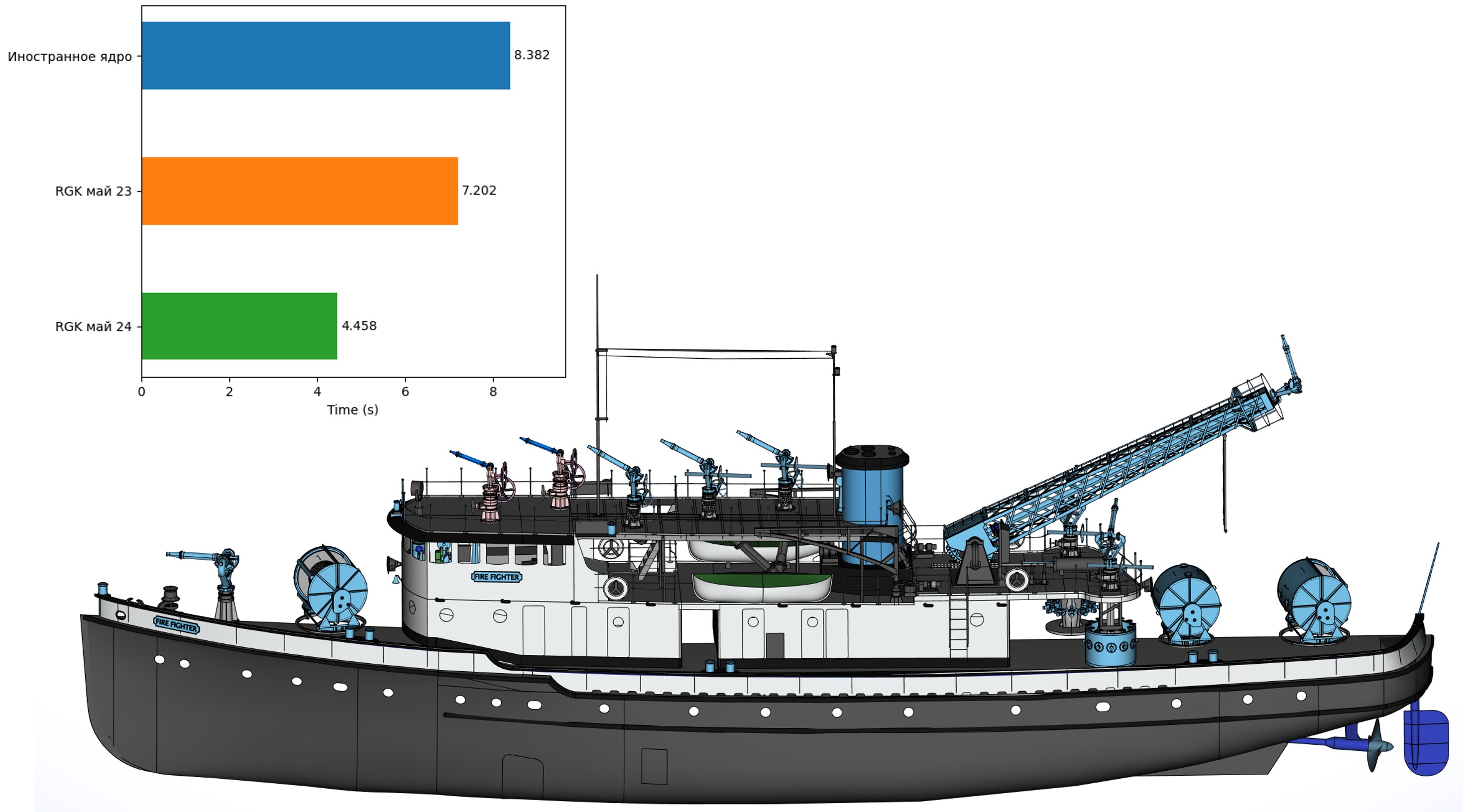
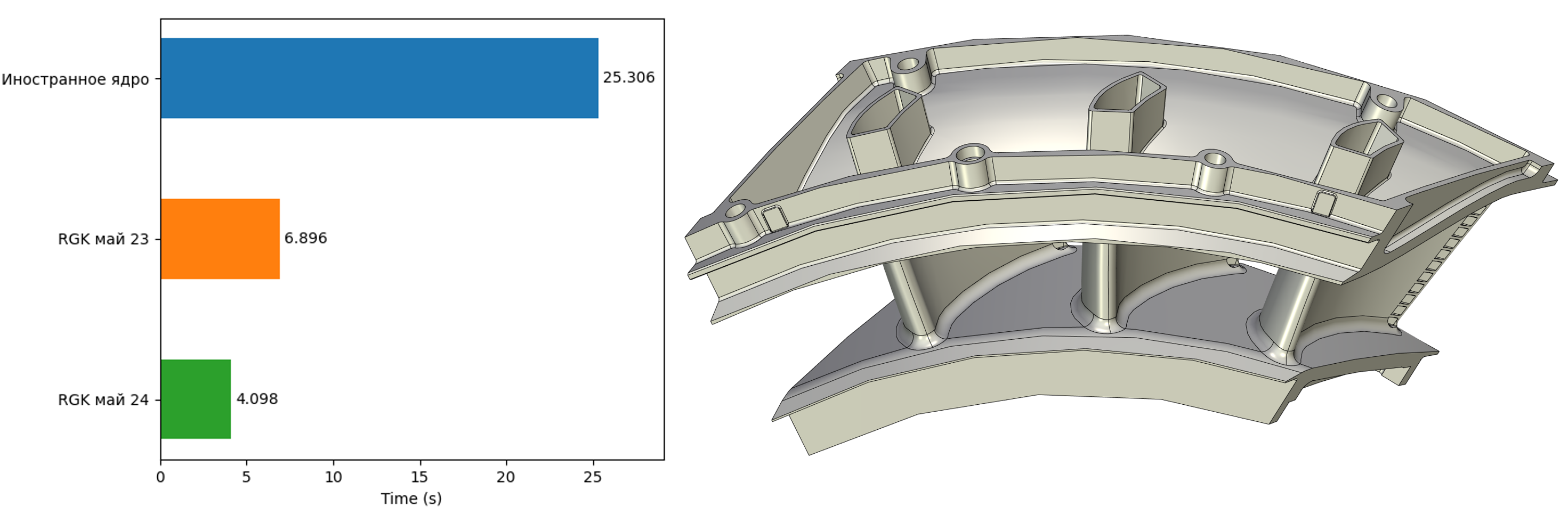
Примеры работы фасетера RGK в сравнении с известным конкурирующим ядром и версией годичной давности
Была проделана значительная работа по улучшению и развитию пользовательского API ядра. В течение года API ядра, по сути, было модернизировано под требования промышленного использования. Новая версия API позволяет поставлять прикладным программистам только релизную библиотеку и файлы заголовков как для отладочных, так и для продуктовых целей. Важным развитием API, на наш взгляд, является появление Python API и его интеграция в том числе в тестовую оболочку ядра. Теперь становится легко писать небольшие прикладные системы с использованием инструментария RGK программистам на языке Python. Разработаны новые алгоритмы идентификации топологических элементов модели – теперь им назначаются идентификаторы фиксированной структуры. Это позволяет значительно упростить взаимодействие прикладного кода с API ядра и уменьшить требования по памяти для хранения ссылок на элементы топологической модели из прикладного кода. Улучшилась документация, примеры использования, тестовое приложение.
Ближайшие планы и направления работ
Как уже отмечалось, сейчас в разработке много полезных и интересных функций и инструментов. Про часть из них было написано выше. Но это не полный перечень работ. В частности, идёт разработка алгоритмов построения серединных поверхностей в разных постановках, в том числе и «истинно» серединных, работающих на произвольной геометрии. Планируются расширение функций и дальнейшее ускорение фасетера, процедуры удаления невидимых линий, проверки пересечений тел, генерации лофт и свип поверхностей со сложными граничными условиями и повышение качества самих поверхностей, возможно снятие ограничений на топологию G2 сглаживаний и много чего ещё. Все описанные работы идут прямо сейчас, а не пишутся в дорожные карты. Так что, как говорится, ждите новостей. Может быть раньше, чем через год.
Ещё одним стимулом для ускорения разработки ядра является постепенный переход флагманского продукта компании «Топ Системы» (T-FLEX CAD) на использование RGK и появление всё большего числа заинтересованных в использовании ядра в своих приложениях компаний разработчиков. В настоящее время уже несколько ведущих российских разработчиков инженерного программного обеспечения ведут опытную эксплуатацию RGK с целью оценки возможности использования ядра в своих разработках при поддержке компании «Топ Системы». Очевидно, что это только начало.
Ядро RGK постоянно развивается и совершенствуется, так как заявленная год назад цель: повысить уровень технологической независимости нашей страны за счёт использования отечественного геометрического ядра, честно конкурирующего с лучшими решениями на мировом рынке, осталась неизменной. Несмотря на амбициозность и крайнюю сложность этой задачи, прошедший год только укрепил уверенность в достижимости этой цели в относительно короткие сроки. Конечно, работы ещё предстоит очень и очень много, как в плане добавления новой функциональности, так и в части повышения скорости и робастности программного кода, но дорогу осилит идущий.












